PRISM-games extends the existing PRISM modelling language to support the specification of stochastic multi-player games. This works differently for the three types of games supported, each of which is explained below. We assume familiarity with the main PRISM modelling language.
See also the case studies and examples sections of this web site for many illustrations and explanations of the PRISM-games modelling language.
Specification of turn-based stochastic multi-player games (SMGs) builds upon the usual modelling of MDPs since they can essentially be seen as a generalisation of MDPs in which each state of the model is controlled by a specific player. A simple example is shown below.
SMG models are indicated by including the keyword smg. The set of players is specified using one or more player ... endplayer constructs, usually at the top of the file. For example, the model below has two players, named p1 and p2. For a turn-based game, it needs to be specified which player controls each state. In PRISM-games, this is done by proving a list of action names and/or module names for each player. This player then controls any state where all the transitions available are either labelled with one of these actions or are unlabelled and belong to one of these modules. For example, player p1 below controls states where there are (synchronous) transitions labelled with send1 or send2 and any asynchronous (unlabelled) transitions from module host. For turn-based games, the occurence of states where the transitions are owned by multiple players results in an error. It is permissible for some actions/modules to not be allocated to any player, as long as multiple such transitions do not occur in any state.
smg player p1 host, [send1], [send2] endplayer player p2 client endplayer module host h : [0..2] init 0; [send1] h=0 -> (h'=1); // send message 1 [send2] h=0 -> (h'=2); // send message 2 [] c=0 -> (h'=0); // restart endmodule module client c : [0..2] init 0; [send1] c=0 -> 0.85 : (c'=1) + 0.15 : (c'=0); // receive message 1 [send2] c=0 -> 0.85 : (c'=2) + 0.15 : (c'=0); // receive message 2 [] c!=0 -> (c'=0); // request another message [] c!=0 -> true; // wait endmodule
The resulting SMG generated by PRISM can be found below. Player 1 states are drawn as diamonds and player 2 states as boxes; states are labelled with with the values of the variables: (h,c ).
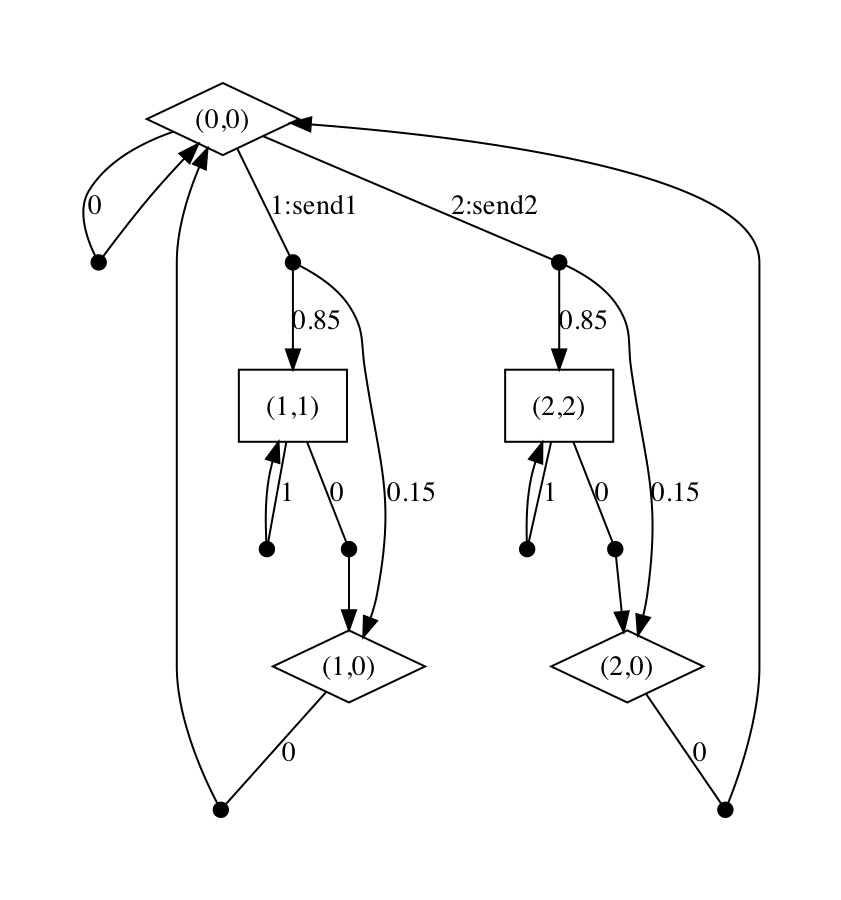
There are more example SMG model files available in the prism-examples/smgs directory included with downloads of PRISM-games.
The simple subdirectory contains some small examples
that can be used to test PRISM-games's functionality for rPATL model checking and strategy synthesis:
Concurrent stochastic multi-player games (CSGs) require a slightly different modelling approach because they are based on the idea that players make choices concurrently in each state, and then make their transitions simultaneously. For a CSG, each player controls one or more modules and the actions that label commands in a player's modules must only be used by that player; this is a little different from PRISM's usual approach to components synchronising on common action labels.
Below, we show an example of a CSG modelling a medium access control system. The model consists of two users with limited energy which share a wireless channel and choose to transmit (t) or wait (w) and, if both transmit, the transmissions fail due to interference. We assume that transmission failure due to collisions is probabilistic, in particular, if a single user transmits, then with probability q1 the transmission succeeds and if both transmit, then with probability q2 there is no collision and transmissions succeed. We also assume that each user has a limited amount of energy, and therefore can only try and transmit their packet a limited number of times.
// CSG model of medium access control // extends model of // Brenguier, R.: PRALINE: A tool for computing Nash equilibria in concurrent games. // In: Proc. CAV’13. LNCS, vol. 8044, pp. 890–895. Springer (2013) // with probability of failure with one or both players transmit csg player p1 mac1 endplayer player p2 mac2 endplayer const int emax; // energy bound const double q1; // probability single user successfully transmits const double q2; // probability two users successfully transmit module channel // used to compute joint probability distribution for transmission failure c : bool init false; // is there a collision? [t1,w2] true -> q1 : (c'=false) + (1-q1) : (c'=true); // only user 1 transmits [w1,t2] true -> q1 : (c'=false) + (1-q1) : (c'=true); // only user 2 transmits [t1,t2] true -> q2 : (c'=false) + (1-q2) : (c'=true); // both users transmit endmodule module mac1 // user 1 s1 : [0..1] init 0; // has player 1 sent? e1 : [0..emax] init emax; // energy level of player 1 [w1] true -> (s1'=0); // wait [t1] e1>0 -> (s1'=c'?0:1) & (e1'=e1-1); // transmit endmodule // construct second user with renaming module mac2 = mac1 [ s1=s2, e1=e2, w1=w2, t1=t2 ] endmodule // reward structure for player 1 rewards "r1" s1=1 : 1; endrewards // reward structure for player 2 rewards "r2" s2=1 : 1; endrewards
CSG models are indicated by including the keyword csg. Each player and the modules of each payer is specified using the player ... endplayer construct.
In this CSG there are two players, corresponding to the two users, which control one module each and, since the behaviour of the two players is the same, module renaming is used to specify the module of the second player. In these modules, the action lists appearing in commands contain a single action, and therefore, since this is the first action in the list, these are the actions of the player controlling the module. To ensure the actions of the different players are distinct we use the index of the player when naming actions. The modules have variables to denote if the users packet has been send and the energy available to the user. A user can only choose to transmit if it has not yet successfully transmitted and it has used up its limited energy supply. Trying to transmit a packet uses up one unit of energy.
Since outcome of transmitting follows a joint probability distribution, we add an addition module not under the control of any player which has a boolean variable which represents the successful transmission and is therefore updated probabilistically based on the action choices of the players. In the commands of the player's own modules which correspond to transmitting we then have updates including the primed value of this boolean variable which also uses the if then else construct.
Specification of turn-based probabilistic timed games (TPTGs) builds upon the existing language for specifying turn-based games in PRISM-games and for probabilistic timed automata (PTAs) in PRISM.
TPTGs are indicated by including the keyword tptg. As for SMGs/TSGs, the set of players is specified using one or more player ... endplayer constructs, which indicate which player controls each location of a TPTG by proving a list of action names and/or module names for each player. The clocks, guards and invariants of a TPTG are specified as for PTAs.
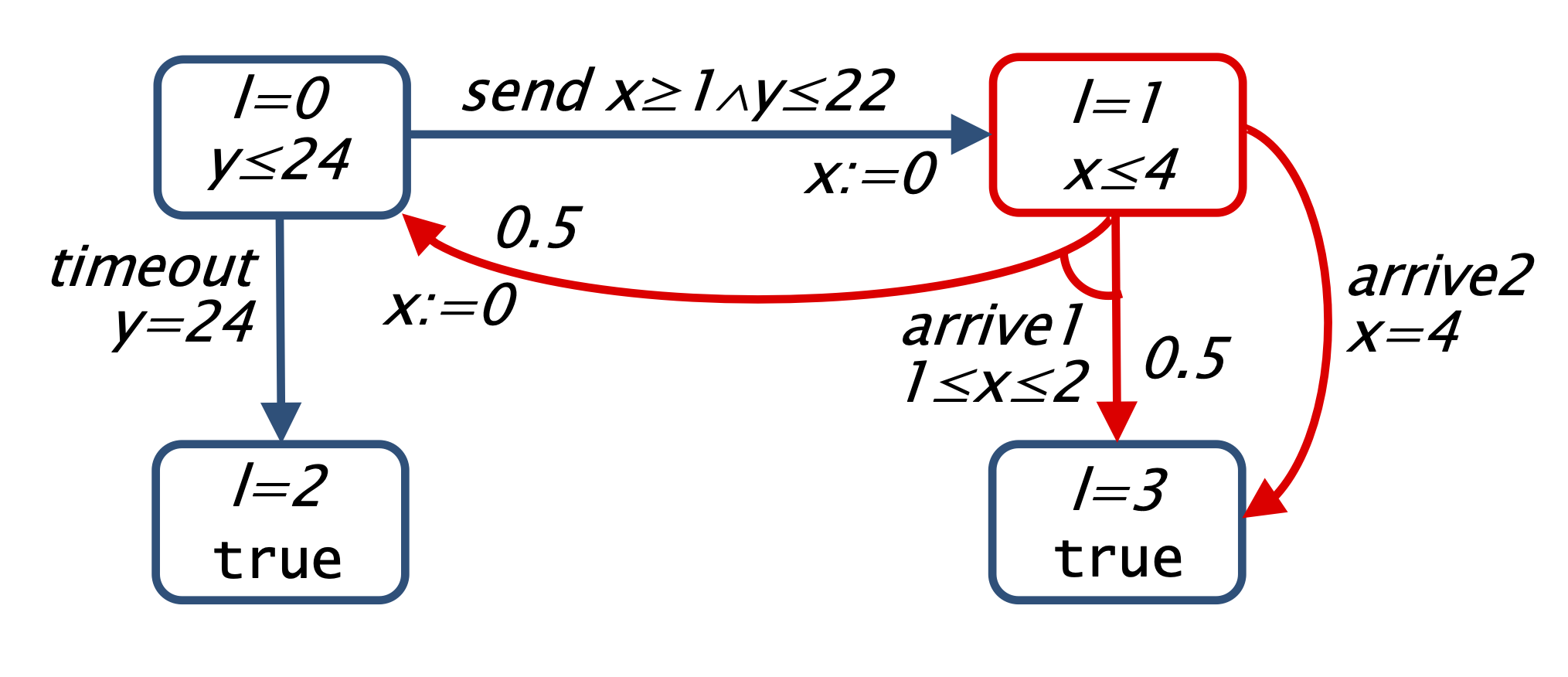
For example, in the TPTG below there are two players: the sender and the medium, with the sender controlling the actions in location l=0 and player medium the actions in location l=1. The TPTG has two clocks: x is used to keep track of the time it takes to send a message and y the elapsed time. In the initial location, the sender waits between 1 and 2 time units before sending the message. The message then passes through the medium that can either delay the message for between 1 and 2 time units after which it arrives with probability 0.5, or delay the message for 4 time units after which it arrives with probability 1. If the message does not arrive, then the sender tries to send it again until reaching a timeout after 24 time units.
// simple tptg model from // Verification and Control of Turn-Based Probabilistic Real-Time Games tptg player sender [send], [timeout] endplayer player medium [arrive1], [arrive2] endplayer module protocol l : [0..3] init 0; // 0 - send // 1 - medium // 2 - fail // 3 - done x : clock; y : clock; invariant (l=0 => (y<=24)) & (l=1 => (x<=4)) endinvariant [send] l=0 & x>=1 & y<=22 -> (l'=1) & (x'=0); [timeout] l=0 & y=24 -> (l'=2); [arrive1] l=1 & x>=1 & x<=2 -> 0.9 : (l'=3) + 0.1 : (l'=0) & (x'=0); [arrive2] l=1 & x=4 -> (l'=3); endmodule
The resulting TPTG can be found below. In the figure the locations and transitions controlled by the sender are coloured blue and those controlled by the medium are coloured red.