This hands-on tool session will introduce you to PRISM. The software should already be installed on the PC lab machines, but if you want to use your own machine, it is easy to download and install.
This tutorial is self-contained, but if you want information about running PRISM, the best source of information is the online manual.
Also available are the slides and model/property files from the introductory talk.
Our first example is a PRISM model of a simple probabilistic algorithm due to Knuth and Yao [KY76] for emulating a 6-sided die with a fair coin. Here is a graphical illustration of the algorithm:
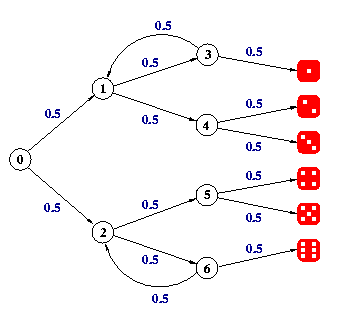
The idea of the algorithm is as follows. Starting from step 0 (i.e. the circle labelled 0), at every step a coin is tossed and there is 50% chance of taking each of the two possible choices. The algorithm terminates when you reach one of the values for the die on the right-hand side.
The PRISM code to model this algorithm is shown below.
dtmc module die // local state s : [0..7] init 0; // value of the die d : [0..6] init 0; [] s=0 -> 0.5 : (s'=1) + 0.5 : (s'=2); [] s=1 -> 0.5 : (s'=3) + 0.5 : (s'=4); [] s=2 -> 0.5 : (s'=5) + 0.5 : (s'=6); [] s=3 -> 0.5 : (s'=1) + 0.5 : (s'=7) & (d'=1); [] s=4 -> 0.5 : (s'=7) & (d'=2) + 0.5 : (s'=7) & (d'=3); [] s=5 -> 0.5 : (s'=7) & (d'=4) + 0.5 : (s'=7) & (d'=5); [] s=6 -> 0.5 : (s'=2) + 0.5 : (s'=7) & (d'=6); [] s=7 -> (s'=7); endmodule
The first line indicates that this model is a discrete-time Markov chain (DTMC). The remaining lines describe a single PRISM module, which we use to model the behaviour of the algorithm. We use two variables to represent the state of the system: s, denoting which step of the algorithm is currently being executed (i.e. which circle in the diagram above), and d, denoting the value of the die (0 means no value has been chosen yet).
The code above should be self-explanatory but, if anything is unclear, you can read the sections on modules/variables and commands in the manual.
Download the model file die.pm for this example from the link above.
Launch the PRISM GUI
and load this file using the "Model | Open model" menu option.
You should see a green tick in the top left corner indicating that the model was loaded successfully.
Click on the "Simulator" tab in the GUI.
You can now use the
simulator
to explore the model.
Create a new path by double-clicking on the main part of the window
(or right-clicking and selecting "New path")
and accept the choice of initial state provided by clicking "OK".
Then, use the "Simulate" button repeatedly to generate a sample execution of the algorithm.
Look at the trace displayed in the main part of the window.
What is the final value of s?
It should be 7. What is the value of the die?
Right-click and select "Reset path".
Then, step through a trace of the algorithm manually
by double-clicking the available transitions
from the "Manual exploration" box.
Try to reach a state where the value of the die is 6.
Now change the value of the "Steps" option under the "Simulate" button from 1 to 20
and, using the "Reset path" option and "Simulate" buttons,
generate several different random traces.
What is the minimum path length you observe? What is the maximum?
We will now use PRISM to perform some analysis of the model.
Download the properties file die.pctl below and then
load it into PRISM using the "Properties | Open properties list" menu option.
const int x; P=? [ F s=7 & d=x ]
The file comprises a constant x, whose value we leave undefined, and one property. The property is of the form P=? [ F phi ] which, intuitively, means "what is the probability, from the initial state of the model, of reaching a state where phi is true?"
What does phi mean in this case?
What does the property mean?
Right click on the property in the GUI and select "Verify".
Pick a value of x between 1 and 6.
Is the answer as you expected?
Click on the "Log" tab to see some additional information that PRISM has displayed regarding the calculations performed.
Read the section in the PRISM manual describing
experiments.
Use PRISM to plot a graph of the value of the property
P=? [ F phi ]
for values of x between 0 and 7.
PRISM also has a discrete-event simulation engine which can be used to generate approximate verification results. This engine is also what underlies the simulator that you used earlier to explore the model manually.
Re-run your experiment using the simulator by ticking the "Use Simulation" option in the experiment dialog.
On the "New Graph Series" dialog, choose to display the results on your existing graph.
In the next dialog, which shows parameters for the simulation process,
you will see that the default number of samples is set to 412042.
Change the number of samples to 10
(if the field is not editable, select a different option from the
"Automatically Calculate" drop-down menu).
How are good are these approximate results?
Keep re-running the experiment, plotting the results on the same graph each time,
and changing the number of samples to 100, 1000, etc.
How many samples do you need to get results close to those generated through verification?
If you want to change the legend or other propeties of the graph, right-click and select "Graph options". You can also export or print the graph from this menu.
We will now use PRISM to compute the expected number of steps that the algorithm being modelled requires to generate a value for the die.
Before you do this, can you compute the result by hand?
You need to add some costs to the model.
In PRISM, we use the terminology "reward", rather than "cost". The two are synonomous.
Go to the "Model" tab of the PRISM GUI and add the following code to the end of the model.
rewards "steps" true : 1; endrewards
This associates a reward of 1 with every state in the model.
Go back to the simulator and generate a random path through the model.
You will see that the reward for each state is now displayed in the table.
Right-click on the path, choose "Configure view" and, from the "Reward visibility" tab,
add the item labelled "cumulative" to the list of visible items
by selecting it from the right-hand panel an clicking the left arrow.
Create another path in the simulator and you will see that the accumulation
of rewards along a path are now also displayed.
We will now use PRISM to compute the expected number of steps. This can be done with a property of the form:
R=? [ F phi ]
which means "what is the expected value of the rewards cumulated, from the initial state of the model, until we reach a state satisfying phi?''.
What should phi be in order to compute
the expected number of steps that the algorithm requries to compute a value for the die?
Go to the "Properties" tab and add this new property to the list of properties.
Verify the property.
Note that you will be prompted for a value of x,
which is not used here so it does not matter what value you specify.
What is the result?
The precise answer is 11/3.
Can you modify the algorithm above so that it emulates a 5-sided die, rather than a 6-sided die?
Run an experiment to show the correctness of your algorithm.
Is this version more or less efficient than the previous one?
We now consider a second example: a self-stabilisation algorithm due to Herman. A self-stabilisation algorithm for a network of processes is a protocol which, when started from some possibly "illegal" start state, returns to a "legal" state without any outside intervention and within some finite number of steps. We call a "legal" state a stable state.
Here is a PRISM model of Herman's algorithm for 7 processes:
// herman's self stabilising algorithm [Her90] // gxn/dxp 13/07/02 // the procotol is synchronous with no nondeterminism (a DTMC) dtmc // module for process 1 module process1 x1 : [0..1] init 1; [step] (x1=x7) -> 0.5 : (x1'=0) + 0.5 : (x1'=1); [step] !(x1=x7) -> (x1'=x7); endmodule // add further processes through renaming module process2 = process1[x1=x2, x7=x1 ] endmodule module process3 = process1[x1=x3, x7=x2 ] endmodule module process4 = process1[x1=x4, x7=x3 ] endmodule module process5 = process1[x1=x5, x7=x4 ] endmodule module process6 = process1[x1=x6, x7=x5 ] endmodule module process7 = process1[x1=x7, x7=x6 ] endmodule // formula, for use in properties: number of tokens // (i.e. number of processes that have the same value as the process to their left) formula num_tokens = (x1=x2?1:0)+(x2=x3?1:0)+(x3=x4?1:0)+(x4=x5?1:0)+(x5=x6?1:0)+(x6=x7?1:0)+(x7=x1?1:0); // rewards (to calculate expected number of steps) rewards "steps" true : 1; endrewards
The processes are arranged in a ring and are identical. Notice how we use PRISM's module renaming facility to avoid duplicating the module definition for each process.
Have a look at the code and work out what a process does at each step of the protocol.
Notice the step action in the square brackets at the start of every command.
This is used to force all 7 processes to synchronise (move simultaneously at each step).
You can read more about synchronisation in the
manual.
Download the model file herman7.pm from above and load it into PRISM.
The state of each process is given by a single 0/1-valued variable. Initially, this value is 1 for all processes (note how this is done in the variable definition in the model file).
What is the maximum possible number of states that this model can be in?
Are all of these states reachable from the initial configuration (1,1,1,1,1,1,1) of the model?
Select the "Model | Build model" menu option
and look at the information displayed in the bottom left of the GUI to find out.
Take a look at the log to see additional information displayed about the model building process.
Download the property file below and load it into PRISM:
// stable states - where only one process has the same value as the process to its left label "stable" = num_tokens=1; // from the initial state, a stable state is reached with probability 1 "init" => P>=1 [ F "stable" ]
For this self-stabilisation algorithm, a stable state is defined as one in which only a single process has a token. A process is said to possess a token if its variable is the same as the process to its left.
Look at the label "stable" which is defined in the file above
and the formula num_tokens from the model file which it uses.
Check that you understand how it relates to the definition of a stable state.
Look at the expressions
section of the manual if not.
Use the PRISM simulator to generate some random paths through the model.
Click on the "stable" label in the top-right part of the simulator
to help you identify which states of these paths are stable.
Note that in this model of the algorithm, we do not actually terminate when a stable state has been reached.
We would like to know whether, from the initial state, a stable state is eventually reached with probability 1.
Check this by verifying the property included in the herman7.pctl file that you loaded into PRISM
(do not forget to deselect the "Use Simulation" option if it is still selected).
If you used a non-probabilistic model checker to verify whether
"from the initial state, a stable state is always eventually reached", what would the result be?
Modify the existing property (double-click or right-click and "Edit") to see if
"the probability of a stable state being reached within 10 steps is (greater than or equal to) 1".
Is it greater than 0.5?
What is the actual probability?
(If you need help, read about the P Operator in the PRISM manual
here
and here.)
Notice that, like in the die example,
we have assigned a reward of 1 to each state of the model.
Create and verify a new property to answer the question
"what is the expected number of steps required for the self-stabilisation algorithm to reach a stable state?".
So far, all our analysis has been for a fixed initial state of the model. We will now carry out a more exhaustive examination of the protocol by considering different classes of initial configuration. PRISM allows a model to have more than one initial state.
Modify the model by removing the "init 1"
part of the definition for variable x1
(and thus also for x2, x3, ... ,x7
since they are defined by renaming).
Add the following code to the end of the model:
init true endinit
Check that the model still builds without errors ("Model | Build model").
Any possible configuration of the process is now considered as an initial state of the model.
Download the following modified properties file and load it into PRISM:
const int k; // states with k tokens label "k_tokens" = num_tokens=k; // stable states - where only one process has the same value as the process to its left label "stable" = num_tokens=1; // maximum expected time to reach a stable state (for all k-token configurations) R=? [ F "stable" {"k_tokens"}{max} ]
This property allows us to compute "the maximum expected time to reach a stable state, starting from any initial configuration in which there are k tokens".
Verify this property for k=7.
Do you get the same value as earlier?
(You should.)
There is an unproven conjecture that, for any number N of processes, the worst-case expected time to reach a stable state always occurs when there are initially 3 tokens. We can't prove this with PRISM, but we can investigate whether it is true for some values of N (in this case, we have N=7 processes).
Create an experiment to compute and plot a graph of the values of the property
for all odd values of k between 1 and 7.
(Again, make sure "Use Simulation" is not still selected.)
[Note: the way that this algorithm works, even numbers of tokens cannot occur.]
Look in the log. You can see exactly which of the various possible configurations result in these worst-case answers.
[Note: in cases where there are more than 10 such configurations, PRISM just prints the first 10.]
For which value of k is the expected time lowest? Why?
For which value is it highest?
Create another PRISM property which computes the minimum expected time to reach a stable state,
starting from any initial configurations in which there are k tokens.
Plot this value for k=1,3,5,7 on a single graph.
This protocol has some other curious properties that can be investigated with PRISM.
In particular, try modifying the algorithm so that the random choice of
each process occurs with probability p,
where p is an undefined constant, rather than 0.5.
Investigate what happens as you vary p.
See here for more details.
This session introduced you to PRISM using two DTMC examples. If you are interested, take a look at some of the other parts of the main PRISM tutorial. This includes:
You can find many more interesting examples in the case studies section of the website.