This tutorial introduces the use of uncertain models for situations where the details of a model are not fully known. More precisely, these models incorporate epistemic uncertainty regarding the transition probabilities between states, for example because they have been learnt from data.
Specifically, PRISM offers support for the analysis of interval MDPs (IMDPs), where transition probabilities are only known to lie within certain intervals. This models, e.g., the situation where transition probabilities were experimentally estimated by confidence intervals.
The main part of this tutorial develops a model of an autonomous drone. However, we begin with an IMDP variant of the model from the robot navigation part of the tutorial:
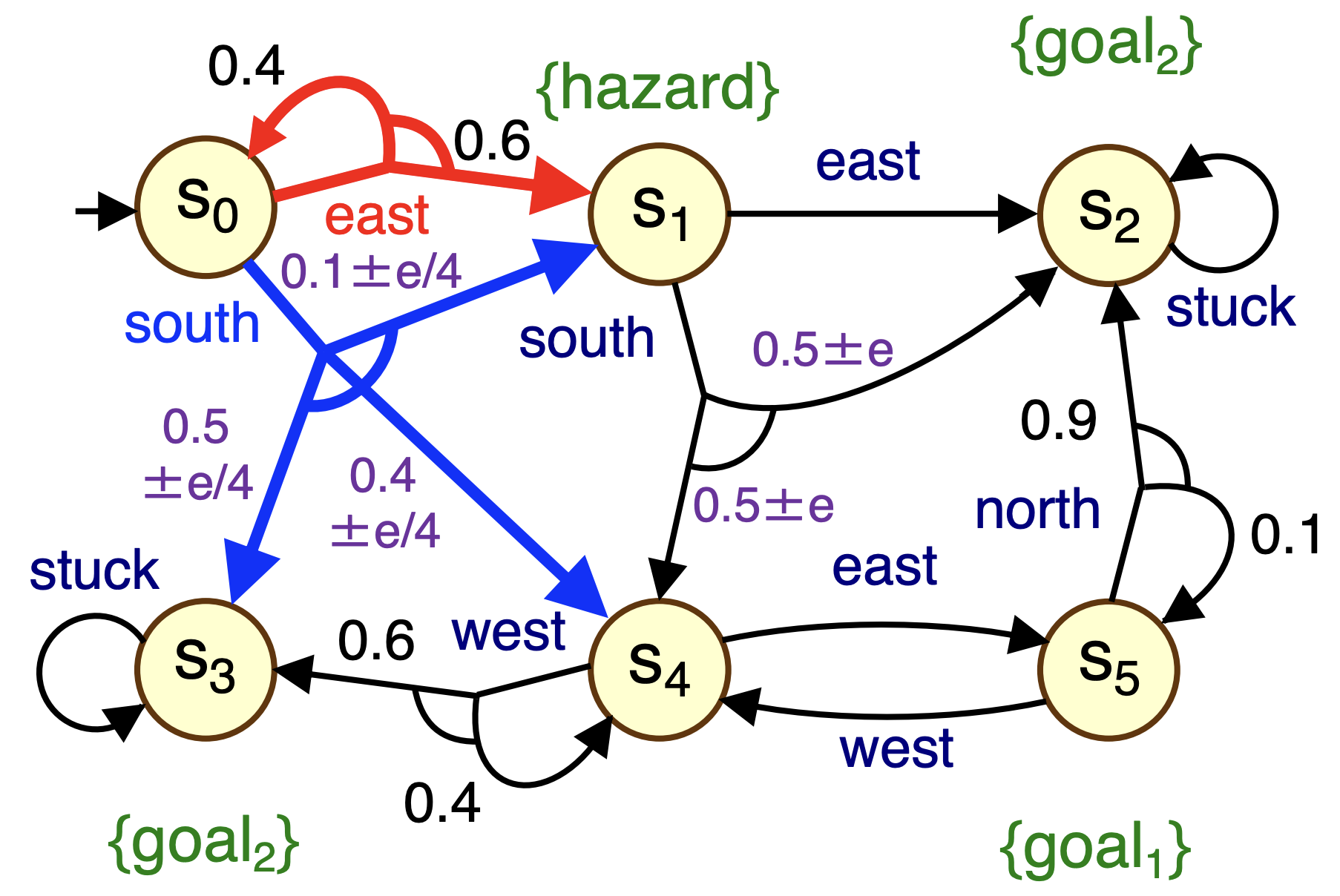
Several of the transitions are marked with intervals, indicating that the actual probabilities could fall anywhere within this range,
 Assume that the parameter e has value 0.2.
Assuming worst-case scenario values for the transition probabilities,
without using PRISM, can you determine how the parameter e
affects the optimal (maximum) probability of reaching a goal1 state?
(you may want to check the earlier part without intervals).
Assume that the parameter e has value 0.2.
Assuming worst-case scenario values for the transition probabilities,
without using PRISM, can you determine how the parameter e
affects the optimal (maximum) probability of reaching a goal1 state?
(you may want to check the earlier part without intervals).
PRISM offers direct support for uncertain transitions defined as intervals (see here for more information):
[a] x=0 -> [0.8,0.9]:(x'=0) + [0.1,0.2]:(x'=1);
The intervals can also include parameters ("constants" in PRISM), which you can define at the top of the model file as:
const double e;
 Model the IMDP above in PRISM, where the transition probability intervals depend on the width parameter e. (Again, consult the earlier robot tutorial for a starting point)
Model the IMDP above in PRISM, where the transition probability intervals depend on the width parameter e. (Again, consult the earlier robot tutorial for a starting point)
We will now use PRISM to analyse the IMDP defined above and extract optimal behavior that is robust with respect to all possibilities induced by the epistemic uncertainty.
Specifications for IMDPs either reason about the worst- or the best-case behavior admissible by the transition intervals, see here.
 Design appropriate specifications for the worst- and the best-case maximum probabilities
of reaching a goal1 state, and verify them in PRISM for different values of e.
What are the probabilities and corresponding optimal policies? What do you observe?
Design appropriate specifications for the worst- and the best-case maximum probabilities
of reaching a goal1 state, and verify them in PRISM for different values of e.
What are the probabilities and corresponding optimal policies? What do you observe?
 In general, which of the two policies obtained for the worst- and the best-case would you ship to the real world?
In general, which of the two policies obtained for the worst- and the best-case would you ship to the real world?
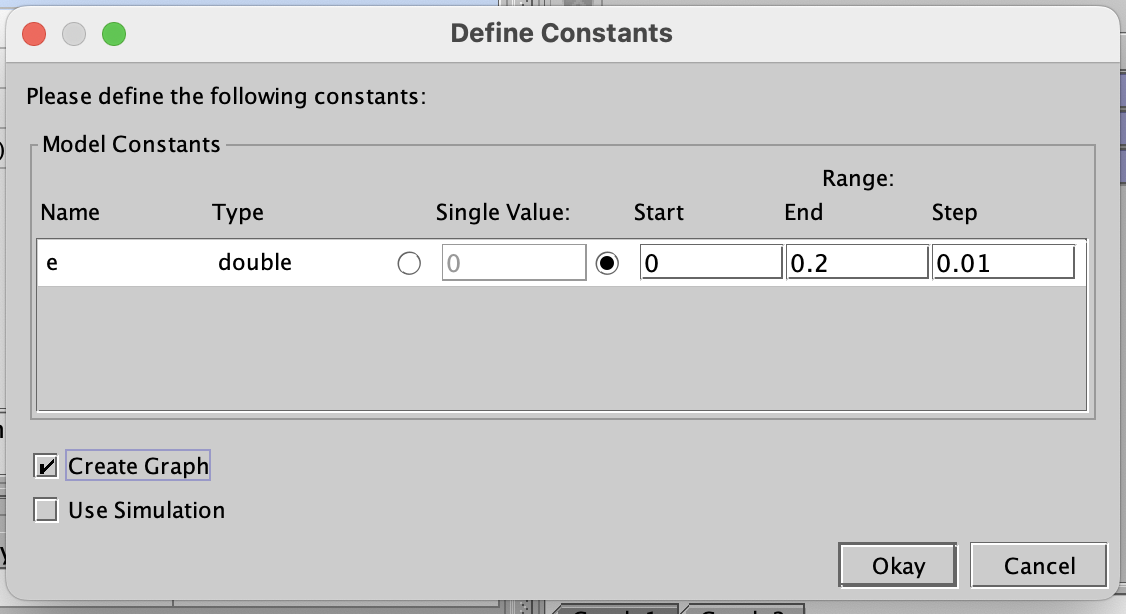
Performing the same operations for multiple constant values, like e above, can be done automatically in PRISM, using the experiments functionality.
 Right-click on the property you want to verify and click "New Experiment".
You should see the following dialogue, allowing you to specify the parameters for the experiment.
Choose a range and a step-size, and make sure that the "Create Graph"
option is ticked.
Right-click on the property you want to verify and click "New Experiment".
You should see the following dialogue, allowing you to specify the parameters for the experiment.
Choose a range and a step-size, and make sure that the "Create Graph"
option is ticked.
If you specified everything correctly for the worst-case probability, you should see a plot similar to:
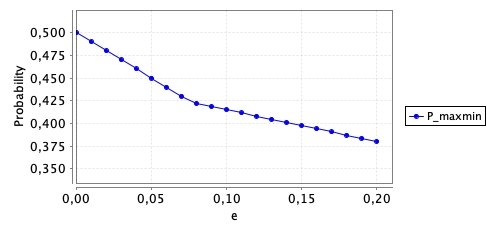
 Can you explain the sharp-bend in the plot?
Can you explain the sharp-bend in the plot?
We now want to analyse how different amounts of epistemic uncertainty can affect optimal robust behaviour. To do so, we consider a more complex example, modelling an autonomous drone.
The environment in which the drone is maneuvering is discretised into a 5 x 6 grid. The drone starts at coordinates (1,1) and is tasked with reaching the goal at (1,6) safely, i.e., without crashing into the obstacles depicted in red.
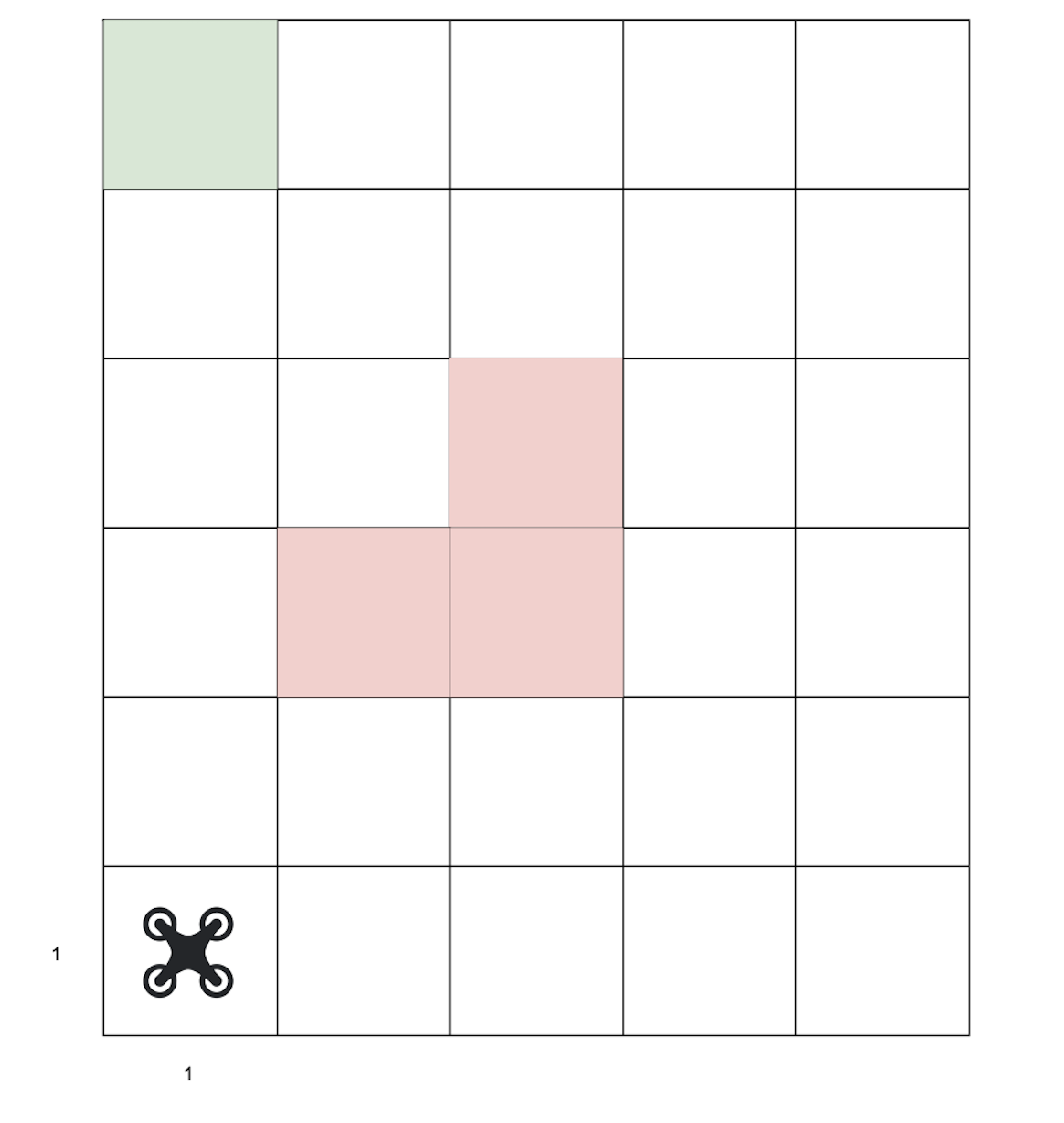
The drone is autonomous, i.e., it operates according to a fixed policy that, for every state (position), may choose to fly straight, left, or right. A complicating factor is that the drone is susceptible to wind, which, with some probability, may push it into an undesired direction or make it not move at all.
The basis for a PRISM model of the drone can be found below.
mdp // Model parameters const double p = 0.1; // Mean disturbance probability const double e; // Epistemic uncertainty formula a = x * e; // Epistemic uncertainty grows with x-coordinate const int M = 5; // Environment width const int N = 6; // Environment height const double eps = 0.0001; // Lower bound for probability ranges // Goal formula goal = x = 1 & y = N; // Obstacles formula crashed = (x = 2 & y = 3) | (x = 3 & y = 3) | (x = 3 & y = 4); // UAV behaviour module env x : [1..M] init 1; y : [1..N] init 1; [up] !crashed & y < N -> [max(eps,1-3*(p+a)), min(1-3*(p-a),1)] : (y'=min(y+1,N)) // Probability to move in intended direction + [max(eps,p-a), min(p+a,1)] : (y'=min(y+1,N)) & (x'=max(x-1,1)) // Probabilities to get pushed by wind + [max(eps,p-a), min(p+a,1)] : (y'=min(y+1,N)) & (x'=min(x+1,M)) + [max(eps,p-a), min(p+a,1)] : true; [right] !crashed & x < M -> [max(eps,1-3*(p+a)), min(1-3*(p-a),1)] : (x'=min(x+1,M)) // Probability to move in intended direction + [max(eps,p-a), min(p+a,1)] : (x'=min(x+1,M)) & (y'=min(y+1,N)) // Probabilities to get pushed by wind + [max(eps,p-a), min(p+a,1)] : (x'=max(x-1,1)) + [max(eps,p-a), min(p+a,1)] : true; [left] !crashed & x > 1 -> [max(eps,1-3*(p+a)), min(1-3*(p-a),1)] : (x'=max(x-1,1)) // Probability to move in intended direction + [max(eps,p-a), min(p+a,1)] : (x'=max(x-1,1)) & (y'=min(y+1,N)) // Probabilities to get pushed by wind + [max(eps,p-a), min(p+a,1)] : (x'=min(x+1,M)) + [max(eps,p-a), min(p+a,1)] : true; endmodule // Your handcrafted policy module policy [up] x < 3 -> true; [left] x >= 3 -> true; [right] false -> true; endmodule // Labelling label "crashed" = crashed; label "goal" = goal;
 Familiarise yourself with the given model.
How is the environment implemented? What happens when the drone encounters an obstacle?
Where does (epistemic) uncertainty come into play, and which effects does it model?
Familiarise yourself with the given model.
How is the environment implemented? What happens when the drone encounters an obstacle?
Where does (epistemic) uncertainty come into play, and which effects does it model?
We want to design policies that maximise the probability of the drone reaching the goal safely and satisfying its task. Before we let PRISM do that automatically, let's take on the role of a UAV engineer and build some policies ourselves. For that, we use a second module (called policy), which interacts with the main module (env) via synchronisation. The policy module uses the same set of actions and only allows the UAV to execute actions when the given conditions are satisfied.
Below is the specification of a (maybe not entirely sensible) policy that controls the drone to fly straight up while the x-coordinate us less than 3, and to fly left in all other cases. Notice that the conditions ("guards") are mutually exclusive and cover the whole state space. Notice also that actions not used by the policy are also present, but with guard false, which disallows the other module from executing those actions independently.
module policy [up] x < 3 -> true; [left] x >= 3 -> true; [right] false -> true; endmodule
 Paste this policy module into the PRISM model above
and simulate some paths through the model to convince yourself that the policy is executed as expected.
Paste this policy module into the PRISM model above
and simulate some paths through the model to convince yourself that the policy is executed as expected.
 For now, let's assume only aleatoric, not epistemic, uncertainty,
i.e., that the probability for the drone to be affected by wind is precisely known in every state.
We can do this in the IMDP by setting e=0.
What is the probability of fulfilliung the task under the policy above?
(Hint: you will need a slightly different property to before, replacing
F "goal"
by !"crashed" U "goal")
For now, let's assume only aleatoric, not epistemic, uncertainty,
i.e., that the probability for the drone to be affected by wind is precisely known in every state.
We can do this in the IMDP by setting e=0.
What is the probability of fulfilliung the task under the policy above?
(Hint: you will need a slightly different property to before, replacing
F "goal"
by !"crashed" U "goal")
 Design a better policy of your own, again under the assumption of no epistemic uncertainty.
What do you observe? Is it better for the drone to fly directly to the goal or to detour around the obstacle?
By how much? Why?
Design a better policy of your own, again under the assumption of no epistemic uncertainty.
What do you observe? Is it better for the drone to fly directly to the goal or to detour around the obstacle?
By how much? Why?
 What is the best policy that you can handcraft, and what performance does it achieve?
Feel free to compare your policies with others in the room.
What is the best policy that you can handcraft, and what performance does it achieve?
Feel free to compare your policies with others in the room.
We now want to take epistemic uncertainty into consideration. Observe that the epistemic uncertainty on the influence of the wind grows with the drone's x-coordinate:
// Model parameters const double p = 0.1; // Mean disturbance probability const double e; // Epistemic uncertainty formula a = x * e; // Epistemic uncertainty grows with x-coordinate
This can be interpreted as having less knowledge about the actual strength/influence of wind the closer that the drone gets to the right border of the environment.
 What influence do the different values of epistemic uncertainty have on the performance of your handcrafted policies?
What influence do the different values of epistemic uncertainty have on the performance of your handcrafted policies?
 For which values of e is it better to choose your policy that flies around
the obstacle, despite less knowledge of the actual behaviour?
And for which values would you choose your policy that flies straight through the obstacle?
For which values of e is it better to choose your policy that flies around
the obstacle, despite less knowledge of the actual behaviour?
And for which values would you choose your policy that flies straight through the obstacle?
 Can you explain and give an interpretation of what you observe?
Can you explain and give an interpretation of what you observe?
 Now, use PRISM to extract the optimal robust policies for different values of epistemic uncertainty.
(You'll need to remove your policy module)
Now, use PRISM to extract the optimal robust policies for different values of epistemic uncertainty.
(You'll need to remove your policy module)
 Are the results similar to what you obtained for your own policies? What is the inflection point of epistemic uncertainty
for which you obtain a higher performance when flying straight through the obstacle? Can you explain? Plot your results and explain them.
Are the results similar to what you obtained for your own policies? What is the inflection point of epistemic uncertainty
for which you obtain a higher performance when flying straight through the obstacle? Can you explain? Plot your results and explain them.
[ Back to index ]