PRISM Modelling

There is no definitive answer to this. Because of PRISM's symbolic implementation, using data structures based on binary decision diagrams (BDDs), its performance can be unpredictable in this respect. There are also several factors that affect performance, including the type of model and property being checked and the engine being used (PRISM has several different engines, which have varying performance).

Having said that, using the default engine in PRISM (the “hybrid” engine), you can normally expect to be able to handle models with up to 10^7-10^8 states on a typical PC. Using the MTBDD engine, you may be able to analyse much larger models (on some of the PRISM case studies, for example, PRISM can do numerical analysis of models with as many as 10^10 or 10^11 states). The manual has more information about PRISM's engines.

The size of a probabilistic model (i.e. the number of states/transitions) is critical to the efficiency of performing probabilistic model checking on it, since both the time and memory required to do so are often proportional to the model size. Unfortunately, it is very easy to create models that are extremely large. Below are a few general tips for reducing model size.

• Look for variables that have unnecessarily large ranges and try to reduce them. Even if your model needs large variables, it is generally a good strategy to first get a smaller version building successfully and then scale it up afterwards.
• Similarly, can you (if only temporarily) reduce the number of modules/components of your model? Start with the smallest number of components possible and then add others one by one.
• Do you have any inter-dependencies between variables? For example, perhaps you have some variables which are simply functions of other variables of the model. Even if these are convenient for model checking, they can be replaced with formulas or labels, which do not contribute to the state space.
• Do any variables include more detail than is necessary for the model? Perhaps this can be exploited in order to reduce the number of variables in your model.
• More generally, are any aspects of the model not relevant to the properties that you are interested in? If so, start with a simpler, more abstract version of the model and then add more details if possible.

Because PRISM is a symbolic model checker, the amount of memory required to store the probabilistic model can vary (sometime unpredictably) according to several factors. One example is the order in which the variables of your model appear in the model file. In general, there is no definitive answer to what the best ordering is but the following heuristics are a good guide.

• Variables which are closely related should appear close together
• Variables which are related to most or all other variables should appear near the start of the ordering

Variables x and y are "related" if, for example, the value of one is has an effect on how the other changes (e.g. (y'=x+1)) or if both appear together in an expression (e.g. a guard).

These heuristics also apply to the ordering of modules within the model file.

For technical details about variable ordering issues, see e.g. section 8 of [HKN+03] or section 4.1.2 of [Par02].

All delays in a CTMC need to be modelled as exponential distributions. This is what makes them efficient to analyse. If you included a transition whose delay was deterministic, i.e. which always occurred after exactly the same delay, the model would no longer be a CTMC.

One solution to this, if your model require such a delay, is to approximate a deterministic delay with an Erlang distribution (a special case of a phase-type distribution). See for example this PRISM model:

In the model, the occurrence of the the go-labelled action occurs with an Erlang distribution with mean mean and shape k. The special case of k=1 is just an exponential distribution. The graph below shows the probability distribution of the delay, i.e. of P=? [ F<=T x=1 ] for different values of k.

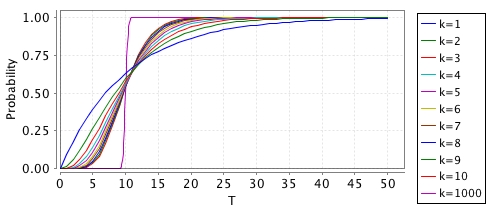
There is an obvious trade-off here between the accuracy (how close it is to modelling a deterministic time delay) and the resulting blow-up in the size of the model that you add this to. For k=1000, you can see that the shape is quite "deterministic" but this would increase your model size by a factor of ~1000.