[Contributed by Ukachukwu Ndukwu and Annabelle McIver]
Related publications: [NM10]
The choice coordination problem (aka distributed consensus) is a typical example of the use of probability for symmetry breaking: identical processes with identical initial conditions must reach an asymmetric state collectively, all choosing one alternative or all choosing the other. The simplest example is a coin flipped between two people in a contest - each has equal chance to win if the coin is fair, the initial conditions are thus symmetric; yet, in the end, one person has won and not the other. In this example, however, the situation is made more complex by insisting that the processes be distributed: they cannot share a central "coin".
A group of tourists are to decide between two meeting places (we call them "left" and "right"). A major constraint is that they may not communicate as a group; nor is there a central "authority" (e.g. a tour guide) whose decision overrides theirs.
Each tourist carries a notepad on which he will write various numbers; outside each of the two potential meeting places is a noticeboard on which various messages will be written. Initially the number zero appears on all the notepads and on the two noticeboards.
Each tourist decides independently (demonically) which meeting place to visit first, after which he strictly alternates his visits between them. At each place he looks at the noticeboard, and if it displays "here'', he goes inside. If it does not display "here'' it will display a number instead, in which case the tourist compares that number K with the number k on his notepad and takes one of the following three actions:
An interesting characterisation of the Rabin's algorithm is that: on termination all the tourists will converge at the same meeting place, and that happens with probability 1.
However, it is not always the case that an "observer" can witness every state of the program that will lead to termination. For example, it is possible that the tourists will forever (according to an observer) keep updating their notepads and the noticeboards without deciding on a meeting place. This behaviour imposes an unbounded state nature on the algorithm.
The tourists’ initial locations are set at verification point. Since the protocol behaviour enforces an unbounded state nature on the algorithm, the constant parameter BOUND helps keep a check on the state explosion of the PRISM model. Below, we show a PRISM implementation for a single tourist. A similar implementation holds for N tourists by simply renaming the tourists’ module parameters.
//Rabin's choice coordination problem //Amended 03/10/2010 //Ensure all tourists' do not start from same location mdp const N = 1; //Number of tourists const t1 = 1; //preset configuration for tourists, 0 --> 'left', 1--> 'right' const int BOUND = 8;//set to manage model size //======== Records update of the left noticeboard ================== module leftboard nlb : [0..BOUND] init 0;//number on left board lbm : [0..1] init 0; //mode of nlb 0 --> 'even', 1 --> 'odd' [t1_nlb_up] (lbm = 0) & (t1_loc = 0) & (lin = 0) & (t1_val = nlb) & (nlb + 3 <= BOUND) -> 0.5 : (nlb' = nlb + 2) & (lbm' = 0) + 0.5 : (nlb' = nlb + 3) & (lbm' = 1); [t1_nlb_up] (lbm = 1) & (t1_loc = 0) & (lin = 0) & (t1_val = nlb) & (nlb + 2 <= BOUND) -> 0.5 : (nlb' = nlb + 2) & (lbm' = 1) + 0.5 : (nlb' = nlb + 1) & (lbm' = 0); endmodule //======== Records update of the right noticeboard ================== module rightboard nrb : [0..BOUND] init 0;//number on right board rbm : [0..1] init 0; //mode of nrb 0 --> 'even', 1 --> 'odd' [t1_nrb_up] (rbm = 0) & (t1_loc = 1) & (rin = 0) & (t1_val = nrb) & (nrb + 3 <= BOUND) -> 0.5 : (nrb' = nrb + 2) & (rbm' = 0) + 0.5 : (nrb' = nrb + 3) & (rbm' = 1); [t1_nrb_up] (rbm = 1) & (t1_loc = 1) & (rin = 0) & (t1_val = nrb) & (nrb + 2 <= BOUND) -> 0.5 : (nrb' = nrb + 2) & (rbm' = 1) + 0.5 : (nrb' = nrb + 1) & (rbm' = 0); endmodule //======== Counts the number of tourists entering the left/right meeting place ================== module counter rin : [0..N] init 0;//number of tourists inside the 'right' meeting place lin : [0..N] init 0;//number of tourists inside the 'left' meeting place [t1_enter_l] (t1_loc = 0) & (flag = 0) & (lin = 0) -> (lin' = lin + 1); [t1_enter_r] (t1_loc = 1) & (flag = 0) & (rin = 0) -> (rin' = rin + 1); [t1_must_l] (t1_loc = 0) & (flag = 0) & (lin > 0) & (lin + 1 <= N) -> (lin' = lin + 1); [t1_must_r] (t1_loc = 1) & (flag = 0) & (rin > 0) & (rin + 1 <= N) -> (rin' = rin + 1); endmodule //======== controls sequence of actions for tourists' at left/right location ================== module semaphore flag : [0..1] init 0; [t1_nlb_up] (flag = 0) -> (flag' = 1); [t1_nrb_up] (flag = 0) -> (flag' = 1); [t1_l_up] (flag = 1) -> (flag' = 0); [t1_r_up] (flag = 1) -> (flag' = 0); endmodule //======== Models the activity of a single tourist ================== module tourist1 t1_loc : [0..2] init t1;// location of tourist 0 --> 'left', 1--> 'right', 2 -->'tourist already in' t1_val : [0..BOUND] init 0;//value on a tourist's notepad t1_com : [0..1] init 0;//tourist's command 0 --> 'idle', 1--> 'active' [t1_nlb_up] (t1_com = 0) & (t1_loc = 0) & (lin = 0) -> (t1_com' = 1); [t1_nrb_up] (t1_com = 0) & (t1_loc = 1) & (rin = 0) -> (t1_com' = 1); [t1_l_up] (t1_com = 1) & (t1_loc = 0) & (lin = 0) -> (t1_val' = nlb) & (t1_loc' = 1) & (t1_com' = 0); [t1_r_up] (t1_com = 1) & (t1_loc = 1) & (rin = 0) -> (t1_val' = nrb) & (t1_loc' = 0) & (t1_com' = 0); [t1_l_copy] (flag = 0) & (t1_loc = 0) & (t1_val < nlb) -> (t1_val' = nlb) & (t1_loc' = 1); [t1_r_copy] (flag = 0) & (t1_loc = 1) & (t1_val < nrb) -> (t1_val' = nrb) & (t1_loc' = 0); [t1_enter_l] (flag = 0) & (t1_loc = 0) & (lin = 0) & (t1_val > nlb) -> (t1_loc' = 2); [t1_enter_r] (flag = 0) & (t1_loc = 1) & (rin = 0) & (t1_val > nrb) -> (t1_loc' = 2); [t1_must_l] (flag = 0) & (t1_loc = 0) & (lin > 0) & (lin + 1 <= N) -> (t1_loc' = 2); [t1_must_r] (flag = 0) & (t1_loc = 1) & (rin > 0) & (rin + 1 <= N) -> (t1_loc' = 2); [t1_l_exit] (flag = 0) & (lin = N) & (t1_loc = 2) -> (t1_val' = t1_val) ; [t1_r_exit] (flag = 0) & (rin = N) & (t1_loc = 2) -> (t1_val' = t1_val) ; endmodule //========== Assigns a reward of 1 if no convergence yet ============= rewards lin != N & rin != N : 1; endrewards
As mentioned earlier, an important characterisation of the Rabin’s algorithm is that, on termination all the tourists converge at the same meeting place, and the probability of convergence is 1. However, given a concrete system representing this algorithm, it is impossible to verify that the convergence condition holds on a model checking platform. This is easily investigated by model checking the PCTL formula
Pmin=? [ F<=T (lin= N | rin = N) ]
i.e. we compute the minimum probability Pmin, that within a finite number of steps T, all the tourists would have converged at the same meeting place.
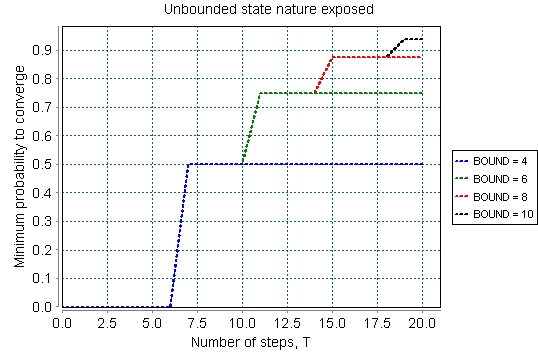
Given a simple scenario consisting of just two tourists (where the first tourist starts at the left and the second at the right door respectively), we see in Fig. 1 that this probability is constrained by the value of the constant parameter BOUND. This also restricts future model checking results of the algorithm to the value of BOUND
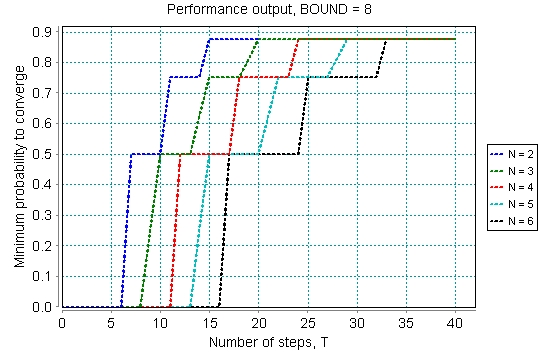
Since we have shown (Fig.1) that the overall performance attribute of the algorithm as captured by the expression above is bounded by the value of the input parameter BOUND, we can therefore study the performance of the algorithm for an N-tourist scenario by setting a value for BOUND prior to verification. We also allow a verifier to set the initial configuration for the tourists’ locations with the proviso that all the tourists cannot start from the same initial location. Fig.2 shows the performance result for N = 2..6 tourists for BOUND = 8.
We also tabulate the minimum and maximum expected number of rounds until the tourists all meet the convergence condition. The reward formula below captures that idea:
Rmin=? [ F (lin= N | rin = N) ] Rmax=? [ F (lin= N | rin = N) ]
where states that have not yet met the convergence condition are worth reward values of 1; we summarize the results below:
| Number of tourists | Rmin | Rmax |
| N = 2 | 4 | Infinity |
| N = 3 | 5 | Infinity |
| N = 4 | 7 | Infinity |
| N = 5 | 8 | Infinity |
| N = 6 | 10 | Infinity |
However, to defeat the overhead incurred by model checking the original (concrete) infinite state protocol by eliminating the BOUND parameter, we have constructed a precise predicate abstraction representation of the protocol. We have similarly reported its performance results for the base cases of even and odd number of tourists. For a detailed description of our abstraction technique and results, readers are referred to [NM10].