(Lehmann and Rabin)
This case study is based on Lehmann and Rabin's [LR81] randomised solution to the well known dining philosophers problem. Note that this protocol has also been studies in [PZ86]. We consider both the original algorithm and the version presented in [DFP04] which removes the need to consider 'fairness' assumptions on the scheduling mechanism.
This algorithm is Lehmann and Rabin's [LR81] solution to the well known dining philosophers problem. The model is represented as an MDP. We let N denotes the number of philosophers. By way of example, the PRISM source code for the original algorithm in the case where N = 3 is given below.
// randomized dining philosophers [LR81] // dxp/gxn 12/12/99 // atomic formulae // left fork free and right fork free resp. formula lfree = (p2>=0&p2<=4)|p2=6|p2=10; formula rfree = (p3>=0&p3<=3)|p3=5|p3=7|p3=11; module phil1 p1: [0..11]; [] p1=0 -> (p1'=0); // stay thinking [] p1=0 -> (p1'=1); // trying [] p1=1 -> 0.5 : (p1'=2) + 0.5 : (p1'=3); // draw randomly [] p1=2 & lfree -> (p1'=4); // pick up left [] p1=2 & !lfree -> (p1'=2); // left not free [] p1=3 & rfree -> (p1'=5); // pick up right [] p1=3 & !rfree -> (p1'=3); // right not free [] p1=4 & rfree -> (p1'=8); // pick up right (got left) [] p1=4 & !rfree -> (p1'=6); // right not free (got left) [] p1=5 & lfree -> (p1'=8); // pick up left (got right) [] p1=5 & !lfree -> (p1'=7); // left not free (got right) [] p1=6 -> (p1'=1); // put down left [] p1=7 -> (p1'=1); // put down right [] p1=8 -> (p1'=9); // move to eating (got forks) [] p1=9 -> (p1'=10); // finished eating and put down left [] p1=9 -> (p1'=11); // finished eating and put down right [] p1=10 -> (p1'=0); // put down right and return to think [] p1=11 -> (p1'=0); // put down left and return to think endmodule // construct further modules through renaming module phil2 = phil1 [ p1=p2, p2=p3, p3=p1 ] endmodule module phil3 = phil1 [ p1=p3, p2=p1, p3=p2 ] endmodule // labels label "hungry" = ((p1>0)&(p1<8))|((p2>0)&(p2<8))|((p3>0)&(p3<8)); label "eat" = ((p1>=8)&(p1<=9))|((p2>=8)&(p2<=9))|((p3>=8)&(p3<=9));
The table below shows statistics for the MDPs we have built for different values of the constants N and K. The tables include:
| N: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | ||||
| 3 | 956 | 3,696 | 910 | 3 | 0.124 | 18 | |||
| 4 | 9,440 | 48,656 | 1,958 | 3 | 0.141 | 24 | |||
| 5 | 93,068 | 599,600 | 3,335 | 3 | 0.311 | 30 | |||
| 6 | 917,424 | 7,092,696 | 5,008 | 3 | 0.782 | 36 | |||
| 7 | 9,043,420 | 81,568,144 | 6,968 | 3 | 1.568 | 42 | |||
| 8 | 89,144,512 | 918,913,056 | 9,215 | 3 | 2.942 | 48 | |||
| 9 | 878,732,012 | 10190,342,448 | 11,749 | 3 | 5.025 | 54 | |||
| 10 | 8,662,001,936 | 111,611,282,280 | 14,570 | 3 | 7.532 | 60 | |||
| 15 | 8.06e+15 | 1.56e+17 | 32,980 | 3 | 37.85 | 90 | |||
| 20 | 7.50e+19 | 1.93e+21 | 58,565 | 3 | 105.3 | 120 | |||
| 25 | 6.98e+24 | 2.24e+26 | 91,325 | 3 | 1,000 | 150 | |||
| 30 | 6.45e+29 | 2.51e+31 | 13,1260 | 3 | 2,719 | 180 | |||
When model checking, we have the following requirement:
This corresponds to the conditions on the adversary/scheduler which we impose by model checking against only fair adversaries.
We have model checked the following liveness property: 'If a philosopher is hungry, then eventually some philosopher eats'.
// liveness (if a philosopher is hungry then eventually some philosopher eats) "hungry" => P>=1 [ true U "eat"]
| N: | Precomputation: | Main Algorithm: | ||||
| Time (s): | Iterations: | Time (s): | Iterations: | |||
| 3 | 0.01 | 6 | - | - | ||
| 4 | 0.03 | 6 | - | - | ||
| 5 | 0.07 | 6 | - | - | ||
| 6 | 0.08 | 6 | - | - | ||
| 7 | 0.13 | 6 | - | - | ||
| 8 | 0.17 | 6 | - | - | ||
| 9 | 0.23 | 6 | - | - | ||
| 10 | 0.29 | 6 | - | - | ||
| 15 | 0.73 | 6 | - | - | ||
| 20 | 1.36 | 6 | - | - | ||
| 25 | 2.20 | 6 | - | - | ||
| 30 | 5.22 | 6 | - | - | ||
This algorithm is the version of Lehmann and Rabin's dining philosopher algorithm presented in [DFP04] and does not require any fairness assumptions. The model is represented as an MDP. We let N denotes the number of philosophers. By way of example, the PRISM source code for the algorithm of [DFP04] in the case of 3 philosophers is given below. The difference between this algorithm and that originally presented by Lehmann and Rabin is that the philosophers cannot be scheduled if their next transition is a 'loop', i.e. such transitions are removed from the model.
// randomized dining philosophers [LR81] // dxp/gxn 23/01/02 // model which does not require fairness // remove the possibility of loops: // (1) cannot stay in thinking // (2) if first fork not free then cannot move (another philosopher must more) mdp // atomic formulae // left fork free and right fork free resp. formula lfree = (p2>=0&p2<=4)|p2=6|p2=10; formula rfree = (p3>=0&p3<=3)|p3=5|p3=7|p3=11; module phil1 p1: [0..11]; [] p1=0 -> (p1'=1); // trying [] p1=1 -> 0.5 : (p1'=2) + 0.5 : (p1'=3); // draw randomly [] p1=2 & lfree -> (p1'=4); // pick up left [] p1=3 & rfree -> (p1'=5); // pick up right [] p1=4 & rfree -> (p1'=8); // pick up right (got left) [] p1=4 & !rfree -> (p1'=6); // right not free (got left) [] p1=5 & lfree -> (p1'=8); // pick up left (got right) [] p1=5 & !lfree -> (p1'=7); // left not free (got right) [] p1=6 -> (p1'=1); // put down left [] p1=7 -> (p1'=1); // put down right [] p1=8 -> (p1'=9); // move to eating (got forks) [] p1=9 -> (p1'=10); // finished eating and put down left [] p1=9 -> (p1'=11); // finished eating and put down right [] p1=10 -> (p1'=0); // put down right and return to think [] p1=11 -> (p1'=0); // put down left and return to think endmodule // construct further modules through renaming module phil2 = phil1 [ p1=p2, p2=p3, p3=p1 ] endmodule module phil3 = phil1 [ p1=p3, p2=p1, p3=p2 ] endmodule // rewards (number of steps) rewards "num_steps" [] true : 1; endrewards // labels label "hungry" = ((p1>0)&(p1<8))|((p2>0)&(p2<8))|((p3>0)&(p3<8)); label "eat" = ((p1>=8)&(p1<=9))|((p2>=8)&(p2<=9))|((p3>=8)&(p3<=9));
The table below shows statistics for the MDPs we have built for different values of the constants N and K. The tables include:
| N: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | ||||
| 3 | 956 | 3,048 | 765 | 3 | 0.065 | 18 | |||
| 4 | 9,440 | 40,120 | 1,650 | 3 | 0.121 | 24 | |||
| 5 | 93,068 | 494,420 | 2,854 | 3 | 0.259 | 30 | |||
| 6 | 917,424 | 5,848,524 | 4,339 | 3 | 0.612 | 36 | |||
| 7 | 9,043,420 | 67,259,808 | 6,101 | 3 | 1.18 | 42 | |||
| 8 | 89,144,512 | 757,721,264 | 8,150 | 3 | 2.31 | 48 | |||
| 9 | 878,732,012 | 8,402,796,252 | 10,486 | 3 | 3.74 | 54 | |||
| 10 | 8,662,001,936 | 92,032,909,540 | 13,109 | 3 | 5.83 | 60 | |||
We have model checked the following properties:
const int K; // discrete time bound // liveness (if a philosopher is hungry then eventually some philosopher eats) "hungry" => P>=1 [ true U "eat"] // bounded waiting (minimum probability, from a state where someone is hungry, that a philosopher will eat within K steps) Pmin=?[true U<=K "eat" {"hungry"}{min}] // expected time (from a state where someone is hungry the maximum exapected number of steps until a philosopher eats) Rmax=?[F "eat" {"hungry"}{max}]
Liveness: the model checking statistics for this property are given below.
| N: | Precomputation: | Main Algorithm: | ||||
| Time (s): | Iterations: | Time (s): | Iterations: | |||
| 3 | 0.03 | 20 | - | - | ||
| 4 | 0.34 | 34 | - | - | ||
| 5 | 1.70 | 54 | - | - | ||
| 6 | 8.20 | 74 | - | - | ||
| 7 | 33.2 | 100 | - | - | ||
| 8 | 122 | 130 | - | - | ||
| 9 | 818 | 166 | - | - | ||
| 10 | 1,673 | 202 | - | - | ||
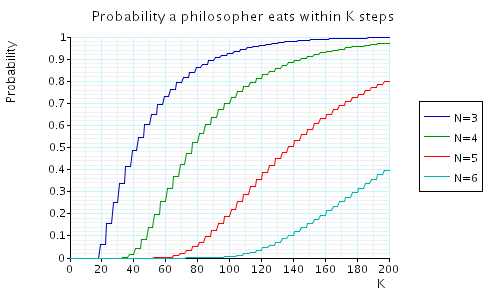
Bounded waiting: in the graph below we have plotted these probabilities as L varies for a range of values of N.
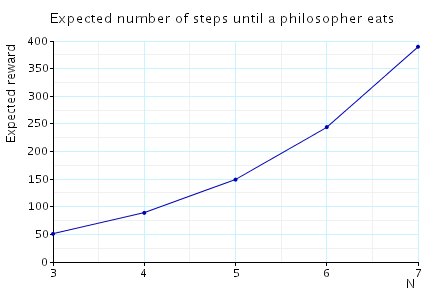
Expected time: in the graph below we have plotted these expected values as N varies.