(Lecca and Priami)
In this case study we consider a probabilistic model of cell cycle control in eukaryotes, a very commonly occurring class of single-celled or multi-cellular organisms. The model is a translation of the formal specification in the biochemical stochastic π-calculus given in [LP03] which studies the relative concentration of a number types of proteins, partaking concurrently in several complex chemical reactions.
In this approach, the time until a reaction between proteins is modelled as an exponential distribution, and therefore we construct a CTMC model of the system where the states of the CTMC correspond to the number of proteins of each type and the transitions correspond to the possible reactions between the proteins. The rate of a reaction is determined by a base rate and the concentrations of the reactants (i.e. the number of each type of molecule that takes part in the reaction).
Note that, for each reaction we consider, the rate of the reaction is the base rate multiplied by the product of the number of elements of each type that take part in the reaction. Therefore, to model this is PRISM, we use the fact that in PRISM the rate of synchronous transition is defined as the product of the rates of the local transitions which form this synchronous transition.
The PRISM source code for this pathway is given below.
// cell cycle control in eukaryotes // based on the stochastic pi caclulus model of Lecca and Priami ctmc // initial number of molecules const int CYCLIN=2*N; const int CDK=N; const int CDH1=N; const int CDC14=2*N; const int CKI=N; const int N; // base rates of reactions const double R1 =0.005; const double R2 =0.001; const double R3 =0.003; const double R4 =0.5; const double R5 =0.3; const double R6 =0.005; const double R7 =0.009; const double R8 =0.009; const double R9 =0.01; const double R10=0.017; const double R11=0.02; // module for including the base rates module base_rates [degp] true -> R1 : true; [degc] true -> R2 : true; [degd] true -> R3 : true; [lb] true -> R4 : true; [bb] true -> R5 : true; [cdh1r] true -> R6 : true; [pcdh1r] true -> R7 : true; [removep] true -> R8 : true; [removecki] true -> R9 : true; [donothing] true -> R10 : true; [bind] true -> R11 : true; endmodule // CYCLIN module cyclin cyclin : [0..CYCLIN] init CYCLIN; cyclin_bound : [0..CYCLIN] init 0; degc : [0..CYCLIN] init 0; trim : [0..CYCLIN] init 0; dim : [0..CYCLIN] init 0; [lb] cyclin>0 & cyclin_bound<CYCLIN -> cyclin : (cyclin_bound'=cyclin_bound+1) & (cyclin'=cyclin-1); [degp] cyclin_bound>0 & degc<CYCLIN -> cyclin_bound : (degc'=degc+1) & (cyclin_bound'=cyclin_bound-1); [degd] cyclin_bound>0 -> cyclin_bound : (cyclin_bound'=cyclin_bound); [bind] cyclin_bound>0 & trim<CYCLIN -> cyclin_bound : (trim'=trim+1) & (cyclin_bound'=cyclin_bound-1); [degc] degc>0 -> degc : (degc'=degc-1); // rate dependent on the number of cyclin/cdk pairs which have a private channel [bb] trim>0 & dim<CYCLIN -> 1 : (dim'=dim+1) & (trim'=trim-1); [removecki] dim>0 & cyclin_bound<CYCLIN -> dim : (cyclin_bound'=cyclin_bound+1) & (dim'=dim-1); [donothing] dim>0 -> dim : (dim'=dim); endmodule // keeps track of the number of cyclin/cdk bounded pairs (i.e. pairs what have a private channel) module counter bound1 : [0..min(CDK,CYCLIN)]; // pairs bound (cyclin has not bound with cki) bound2 : [0..min(CDK,CYCLIN)]; // pairs bound (cyclin bound with cki) [lb] bound1<min(CDK,CYCLIN) -> (bound1'=bound1+1); [degp] cyclin_bound>0 & bound1<=cyclin_bound -> bound1/cyclin_bound : (bound1'=bound1-1) // probability cyclin which is bound takes part in the reaction + 1-bound1/cyclin_bound : true; // probability cyclin which is not bound takes part in the reaction [bind] cyclin_bound>0 & bound1<=cyclin_bound & bound2<min(CDK,CYCLIN) -> bound1/cyclin_bound : (bound1'=bound1-1) & (bound2'=bound2+1) // probability cyclin which is bound takes part in the reaction + 1-bound1/cyclin_bound : true; // probability cyclin which is not bound takes part in the reaction [degc] cdk_cat>0 & bound1+bound2<=cdk_cat -> bound1/cdk_cat : (bound1'=bound1-1) // probability cdk which is bound (and corresponding cyclin not bound to cki) takes part in the reaction + bound2/cdk_cat : (bound2'=bound2-1) // probability cdk which is bound (and corresponding cyclin bound to cki) takes part in the reaction + 1-(bound1+bound2)/cdk_cat : true; // probability cdk which is not bound takes part in the reaction [bb] bound2>0 -> bound2 : (bound2'=bound2-1); endmodule // CDK module cdk cdk : [0..CDK] init CDK; cdk_cat : [0..CDK] init 0; [lb] cdk>0 & cdk_cat<CDK -> cdk : (cdk_cat'=cdk_cat+1) & (cdk'=cdk-1); [cdh1r] cdk_cat>0 -> cdk_cat : (cdk_cat'=cdk_cat); [degc] cdk_cat>0 & cdk<CDK -> cdk_cat : (cdk'=cdk+1) & (cdk_cat'=cdk_cat-1); [bb] cdk_cat>0 -> 1 : (cdk_cat'=cdk_cat-1); // rate dependent on the number of cyclin/cdk pairs which have a private channel [removecki] cdk<CDK -> 1 : (cdk'=cdk+1); endmodule // CDH1 module cdh1 cdh1 : [0..CDH1] init CDH1; inact : [0..CDH1] init 0; [degp] cdh1>0 -> cdh1 : (cdh1'=cdh1); [cdh1r] cdh1>0 & inact<CDH1 -> cdh1 : (cdh1'=cdh1-1) & (inact'=inact+1); [removep] cdh1>0 -> cdh1 : (cdh1'=cdh1); [pcdh1r] inact>0 & cdh1<CDH1 -> inact : (inact'=inact-1) & (cdh1'=cdh1+1); endmodule // CDC14 module cdc14 cdc14 : [0..CDC14] init CDC14; [pcdh1r] cdc14>0 -> cdc14 : (cdc14'=cdc14-1); [removep] cdc14<CDC14 -> (CDC14-cdc14) : (cdc14'=cdc14+1); endmodule // CKI module cki cki : [0..CKI] init CKI; [degd] cki>0 -> cki : (cki'=cki-1); [bind] cki>0 -> cki : (cki'=cki-1); endmodule // reward structure: abound of cdc14 rewards "cdc14" true : cdc14; endrewards // reward structure: abound of cdh1 rewards "cdh1" true : cdh1; endrewards // reward structure: abound of cyclin bound rewards "cyclin_bound" true : cyclin_bound; endrewards
The table below shows statistics for the CTMCs we have built for different numbers values of the constants N1 and N2. The tables include:
| N: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | ||||
| 2 | 4,666 | 18,342 | 6,880 | 31 | 0.317 | 27 | |||
| 3 | 57,667 | 305,502 | 22,406 | 48 | 1.627 | 40 | |||
| 4 | 431,101 | 2,742,012 | 81,145 | 78 | 10.025 | 53 | |||
| 5 | 2,326,666 | 16,778,785 | 179,015 | 105 | 32.997 | 66 | |||
| 6 | 9,960,861 | 78,768,799 | 352,833 | 139 | 86.077 | 79 | |||
We analyse this pathway through the following properties:
These property can be specified by the following CSL formula:
const double t; // time bound const int k; // number of molecules // amount of cyclin bound at time t P=? [ true U[t,t] cyclin_bound=k ] // expected reward at time t R{"cdc14"}=? [I=t] R{"cdh1"}=? [I=t] R{"cyclin_bound"}=? [I=t]
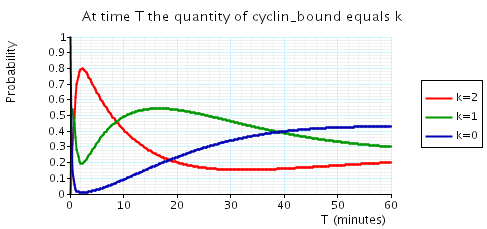
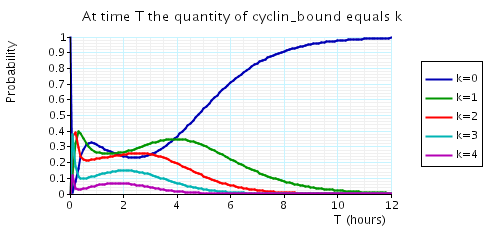
The following graph plots, in the cases when N equals 2, 3 and 4, the probability that there are k cyclin_bound elements at time as the value of T varies.
N = 2
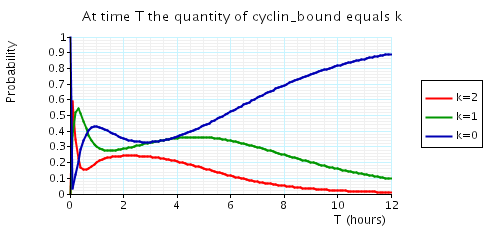
N = 3
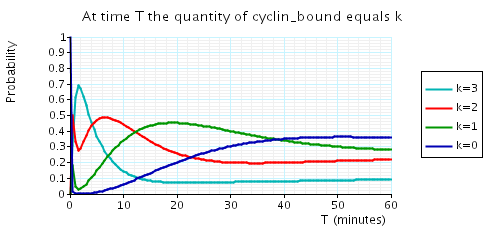
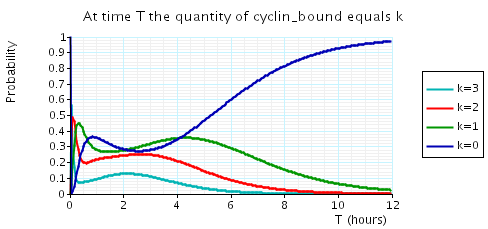
N = 4
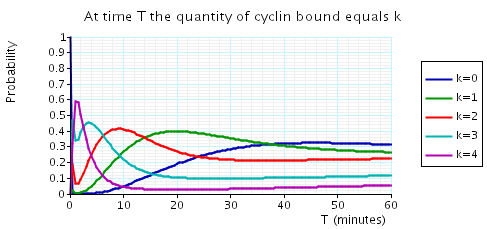
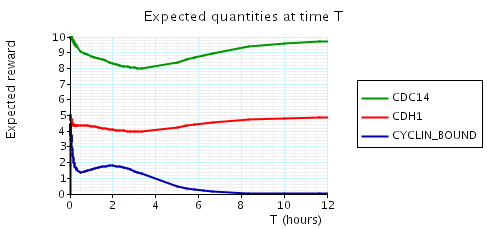
In the graph below we have plotted the above expected values as T varies.
N = 2
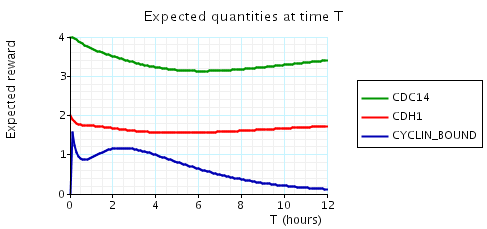
N = 3
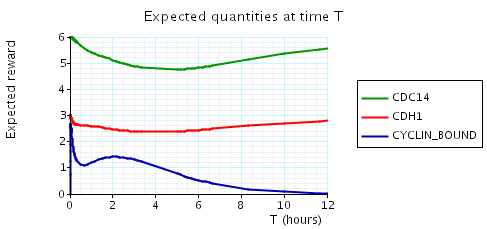
N = 4
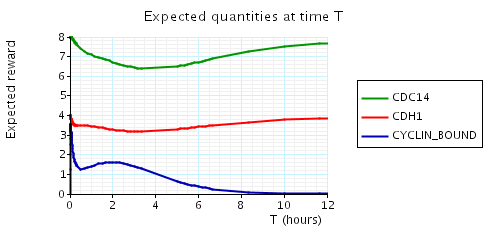
N = 5