(Even, Goldreich & Lempel)
Related publications: [NS06]
Consider several parties on a computer network who wish to exchange some items of value but do not trust each other to behave honestly. Fair exchange is the problem of exchanging data in a way that guarantees that either all participants obtain what they want, or none do. Contract signing is a particular form of fair exchange, in which the parties exchange commitments to a contract (typically, a text string spelling out the terms of the deal). Commitment is often identified with the party's digital signature on the contract. In commercial transactions conducted in a distributed environment such as the Internet, it is sometimes difficult to assess a counter-party's trustworthiness. Contract signing protocols are, therefore, an essential piece of the e-commerce infrastructure.
The main property a contract signing protocol should guarantee is fairness. Informally, a protocol between A and B is fair for A if, in any situation where B has obtained A's commitment, A can obtain B's commitment regardless of B's actions. Ideally, fairness would be guaranteed by the simultaneous execution of commitments by the parties. In a distributed environment, however, simultaneity cannot be assured unless a trusted third party is involved in every communication. Protocols for contract signing are inherently asymmetric, requiring one of the parties to make the first move and thus put itself at a potential disadvantage in cases where the other party misbehaves.
In this case study, we focus on the contract signing protocol of Even, Goldreich, and Lempel [EGL85] (the EGL protocol). In the EGL protocol, each party starts by generating a sequence of pairs of secrets and revealing the encryptions of the contract under each secret. A party is considered committed if the opponent knows both secrets in at least one pair. In the first phase, the parties use oblivious transfer to probabilistically reveal one secret from each pair. In the second phase, they release all secrets bit by bit.
For this protocol as specified in [EGL85], we demonstrate that, with probability 1, it reaches a state in which the responder (second mover) knows both secrets from at least one of the initiator's pairs, but the initiator does not know both secrets from any of the responder's pairs. We use PRISM to quantify the initiator's computational disadvantage by calculating the expected number of bits he needs to guess to complete one of the responder's pairs. For the case when the responder does not stop communicating immediately after reaching a point of advantage, we calculate the expected number of messages that must be exchanged before fairness is restored, that is, the initiator learns both secrets in at least one of the responder's pairs.
We also consider alternative message scheduling schemes for the second phase of the EGL protocol, and present fairness analysis for several variants. We are interested in two questions. First, for a given party P (initiator or responder), what is the probability of reaching a state where the other party knows both secrets from one of P's pairs, but P does not know both secrets from one of the opponent's pairs? (Obviously, we would like this probability to be as close to 1/2 as possible). Second, after an "unfair" state is reached, how long does it take before fairness is restored, that is, how many bits does the "losing" party need to receive before he knows both of the opponent's secrets?
The probabilistic contract signing protocol of Even, Goldreich, and Lempel [EGL85] proceeds as follows. Initiator A generates 2n random secret a1,...,a2n and reveals:
where c is the text of the contract and F(ai,c) can be thought of, roughly, as encryption of c under secret ai. The assumption is that F is uniformly secure cryptosystem (see below). Similarly, B generates 2n random secrets b1,...,b2n, and reveals:
Intuitively, both A's and B's sequences of secrets can be thought of as sequence of pairs { (ai,an+i) } and { (bi,bn+i) }, respectively.
A is considered committed to contract c if B can present both secrets from any one of A's pairs, that is, if B knows both ai and an+i for some i. B is considered committed if A can present bj and bn+j for some j. The secrets can be verified by using them to decrypt the publicly announced values:
that is, they should decrypt to c.
The protocol itself consists in partial secret exchange as presented in below. At the end of the exchange, if both parties behave correctly, B learns all of A's secrets, and vice versa.
|
EGL (A,B,{ (ai,an+i) },{ (bi,bn+i) }) (step 1) for i=1 to n OT(A,B,ai,an+i) (A sends ai and an+i to B via OT) OT(B,A,bi,bn+i) (B sends bi and bn+i to A via OT) end (step 2) for i=1 to L (L is the length of each of the secrets) for j=1 to 2n A transmits bit i of the secret j end for j=1 to 2n B transmits bit i of the secret j end end |
The EGL protocol assumes the existence of a uniformly secure cryptosystem F. Informally, given c, F(k,c) and first i bits of k, the expected time of computing k is independent of the i known bits. In particular, there exists an algorithm A which, given a pair c, F(k,c), finds k in expected time tA(s) where s is an i-bit string consistent with k (s represents partial knowledge of the key k), and tA(s) depends only on the number of unknown bits in k, that is,
for each bit string s of length i consistent with k. Moreover, there is no algorithm that achieves this in less than half the time. A precise definition can be found in [EGL85] (section 2).
The EGL protocol also assumes the existence of a 1-out-of-2 oblivious transfer protocol (OT). The protocolOT(S,R,x,y) can be defined axiomatically as a protocol in which:
We omit the discussion of how such a primitive can be implemented, and assume for the purposes of our analysis that a correct implementation is available.
In our model for the EGL protocol, the state of each party is represented by its current knowledge of the secrets of the other party. More precisely, for party A (B), it is the number of bits of each of the secrets b1,...,b2n (a1,...,a2n) that it have been sent by B (B) in either step 1, or step 2 of the protocol. Therefore, in our PRISM specification we encode the state of the party A with the variables b1,...,b2n (each taking values in the range {0,...,L}) where bi represents the current number of bits of the secret bi that A possesses. These variables are updated when A receives a message from B. The update depends on the type of transmission B performs. For example:
To specify this protocol in PRISM, we define a module for each party (which updates the above variables) and an additional module that is used to keep track of what messages have been sent and the order in which these transmissions take place, that is, how far the parties have actually progressed through the protocol. Following this approach, the specification of the EGL protocol used as the input to PRISM in the case when n=5 and L=2 is given below.
// Randomized Protocol for Signing Contracts [Even, Goldreich and Lempel 1985] // Gethin Norman and Vitaly Shmatikov 2004 dtmc // CONSTANTS const int N=5; // number of pairs of secrets const int L=2; // number of bits in each secret // FORMULE // B knows a pair of secrets formula kB = ( (a0=L & a5=L) | (a1=L & a6=L) | (a2=L & a7=L) | (a3=L & a8=L) | (a4=L & a9=L)); // A knows a pair of secrets formula kA = ( (b0=L & b5=L) | (b1=L & b6=L) | (b2=L & b7=L) | (b3=L & b8=L) | (b4=L & b9=L)); module protocol b : [1..L]; // counter for current bit to be send n : [0..N-1]; // counter for which secret to send phase : [1..4]; // phase of the protocol // 1 - sending secrets using OT (step 1 of the protocol) // 2 - send bits of the secrets 0,...,N-1 (step 2 of the protocol) // 3 - send bits of the secrets N,...,2N-1 (step 2 of the protocol) party : [1..2]; // which party sends next (1 - A and 2 - B) // STEP 1 // A sends [receiveB] phase=1 & party=1 -> (party'=2); // B sends and we move onto the next secret [receiveA] phase=1 & party=2 & n<N-1 -> (party'=1) & (n'=n+1); // B sends and finished this step [receiveA] phase=1 & party=2 & n=N-1 -> (party'=1) & (phase'=2) & (n'=0); // STEP 2 (A sends) // next secret [receiveB] (phase=2 | phase=3) & party=1 & n<N-1-> (n'=n+1); // move onto secrets N,...,2N-1 [receiveB] phase=2 & party=1 & n=N-1 -> (phase'=3) & (n'=0); // move onto party B [receiveB] phase=3 & party=1 & n=N-1 -> (phase'=2) & (party'=2) & (n'=0); // STEP 2 (B sends) // next secret [receiveA] (phase=2 | phase=3) & party=2 & n<N-1 -> (n'=n+1); // move onto secrets N,...,2N-1 [receiveA] phase=2 & party=2 & n=N-1 -> (phase'=3) & (n'=0); // move onto next bit [receiveA] phase=3 & party=2 & n=N-1 & b<L -> (phase'=2) & (party'=1) & (n'=0) & (b'=b+1); // finished protocol [receiveA] phase=3 & party=2 & n=N-1 & b=L -> (phase'=4); // FINISHED [] phase=4 -> (phase'=4); // loop endmodule module partyA // bi the number of bits of B's ith secret A knows // (keep pairs of secrets together to give a more structured model) b0 : [0..L]; b5 : [0..L]; b1 : [0..L]; b6 : [0..L]; b2 : [0..L]; b7 : [0..L]; b3 : [0..L]; b8 : [0..L]; b4 : [0..L]; b9 : [0..L]; // first step (get either secret i or (N-1)+i with equal probability) [receiveA] phase=1 & n=0 -> 0.5 : (b0'=L) + 0.5 : (b5'=L); [receiveA] phase=1 & n=1 -> 0.5 : (b1'=L) + 0.5 : (b6'=L); [receiveA] phase=1 & n=2 -> 0.5 : (b2'=L) + 0.5 : (b7'=L); [receiveA] phase=1 & n=3 -> 0.5 : (b3'=L) + 0.5 : (b8'=L); [receiveA] phase=1 & n=4 -> 0.5 : (b4'=L) + 0.5 : (b9'=L); // second step (secrets 0,...,N-1) [receiveA] phase=2 & n=0 -> (b0'=min(b0+1,L)); [receiveA] phase=2 & n=1 -> (b1'=min(b1+1,L)); [receiveA] phase=2 & n=2 -> (b2'=min(b2+1,L)); [receiveA] phase=2 & n=3 -> (b3'=min(b3+1,L)); [receiveA] phase=2 & n=4 -> (b4'=min(b4+1,L)); // second step (secrets N,...,2N-1) [receiveA] phase=3 & n=0 -> (b5'=min(b5+1,L)); [receiveA] phase=3 & n=1 -> (b6'=min(b6+1,L)); [receiveA] phase=3 & n=2 -> (b7'=min(b7+1,L)); [receiveA] phase=3 & n=3 -> (b8'=min(b8+1,L)); [receiveA] phase=3 & n=4 -> (b9'=min(b9+1,L)); endmodule // construct module for party B through renaming module partyB=partyA[b0=a0,b1=a1, b2=a2,b3=a3, b4=a4,b5=a5, b6=a6,b7=a7, b8=a8,b9=a9, receiveA=receiveB] endmodule
The table below shows statistics for the DTMCs we have built for different numbers values of the constants N and L. The tables include:
| N: | L: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | |||||
| 5 | 2 | 28,830 | 29,853 | 4,207 | 3 | 0.232 | 51 | |||
| 4 | 69,790 | 70,813 | 11,406 | 3 | 0.736 | 91 | ||||
| 6 | 110,750 | 111,773 | 16,235 | 3 | 1.553 | 131 | ||||
| 8 | 151,710 | 152,733 | 29,082 | 3 | 3.65 | 171 | ||||
| 10 | 2 | 55,584,766 | 56,633,341 | 15,332 | 3 | 1.46 | 101 | |||
| 4 | 139,470,846 | 140,519,421 | 42,117 | 3 | 5.25 | 181 | ||||
| 6 | 223,356,926 | 224,405,501 | 59,907 | 3 | 10.6 | 261 | ||||
| 8 | 307,243,006 | 308,291,581 | 108,175 | 3 | 23.1 | 341 | ||||
| 15 | 2 | 8.3e+10 | 8.4e+10 | 33,296 | 3 | 4.35 | 151 | |||
| 4 | 2.1e+11 | 2.1e+11 | 91,843 | 3 | 16.6 | 271 | ||||
| 6 | 3.4e+11 | 3.4e+11 | 130,570 | 3 | 33.3 | 391 | ||||
| 8 | 4.7e+11 | 4.7e+11 | 236,435 | 3 | 72.9 | 511 | ||||
| 20 | 2 | 1.1e+14 | 1.1e+14 | 58,129 | 3 | 10.4 | 201 | |||
| 4 | 2.9e+14 | 2.9e+14 | 160,668 | 3 | 38.6 | 361 | ||||
| 6 | 4.7e+14 | 4.7e+14 | 228,362 | 3 | 76.3 | 521 | ||||
| 8 | 6.4e+14 | 6.4e+14 | 414,054 | 3 | 175 | 681 | ||||
When investigating the EGL protocol, we discovered what might be considered to be a weakness in the protocol when party B is allowed to act maliciously by quitting the protocol early (note that this type of behaviour was not considered in [EGL85]). More precisely, our PRISM analysis shows that, with probability 1, the protocol reaches a state where B possesses both secrets from at least one of A's pairs, while A does not have complete knowledge of any pair of B's secrets. This corresponds to checking that the initial state satisfies the PCTL property:
Intuitively, this happens because in the last round of step 2 of the protocol, A sends the last bit for all of his secrets before B sends the last bit for even a single secret.
This means that if B stops participating in the protocol (that is, stops sending messages to A) as soon as he has obtained at least one of A's pairs, then B enjoys a distinct advantage over A: he knows a pair of A's secrets, while A does not know both secrets in any of B's pairs. This advantage is limited by the fact that in the state where B obtains the last bit he needs to complete a pair of A's secrets, A possesses, for any pair of B's secrets, one complete secret and L-1 bits of the other secret. This means that A can compute the bit that he requires to obtain full knowledge of a pair of B's secrets in expected time TA(|k|-1). This computation will take time, however. Also, supposing that A is behaving honestly, A will wait for B to send a message before realizing that B has quit the protocol and trying to compute B's secret on his own.
An alternative, more general formulation of (un)fairness could be based on the number of bits that each party still has to compute before he, too, knows both secrets in at least one of his opponent's pairs (this is different from the definition in [EGL85], which uses expected time). We say that party A (B) has l-knowledge (0 ≤ l ≤ L) if there exists a pair of secrets (bi,bn+i) ((ai,an+i)) such that A (B) fully knows one of the secrets and at least l bits of the other secret.
Our analysis shows that, with probability 1, for any 1 ≤ l ≤ L the protocol reaches a state where B has l-knowledge, while A does not. In particular, considering the case when l=L (that is, both secrets are completely known), we obtain that, with probability 1, the protocol reaches a state where B knows one of A's pairs while A does know any of B's pairs. All of our subsequent analyses of EGL variants can be generalized in the same way, by replacing "knowledge of a pair of secrets" with "l-knowledge" for any 1 ≤ l ≤ L.
Recall that the weakness we have discovered in the EGL protocol is due to the fact that in step 2, A reveals the last bit for each of his secrets before B reveals any of the last bits of B's secrets. Therefore, B always gains full knowledge of all of A's secrets before A learns even a single pair of B's secrets. We now investigate whether the protocol can be made more fair by considering alternative message scheduling schemes for step 2 of the protocol.
We now consider a number of alternative protocols to EGL where the only difference is the message sequence scheme used in step 2, i.e. step 1 of each protocol is identical to that of the original EGL protocol. The idea behind these alternatives is that they attempt, in varying degrees, to overcome A's "first-mover" disadvantage without becoming unfair towards B.
In the original EGL protocol, the message schedule in step 2 involves A sending the jth bit for all of his secrets before B does the same, and then moving to the next bit.
The scheduling scheme used in EGL2 differs from the original protocol by having B send a bit for each of the secrets 1,...,n after A has done this, and before either party has sent the bits for the secrets n+1,...,2n. The PRISM code for this protocol when n=5 and L=2 can be found here.
The other two schemes we consider (EGL3 and EGL4) separate the sending of the bits for the secrets 1,...,n from those for the secrets n+1,...,2n. More precisely, in these schemes both parties send all the bits for the secrets 1,...,n before they start sending the bits for the secrets n+1,...,2n.
The scheme in EGL3 achieves this by interleaving the exchange bit by bit.
In EGL4 the message schedule of step 2 requires A to send a bit for his first secret and then wait for B to send a bit for each of his secrets 1,...,n, before moving to A's secrets 2,...,n.
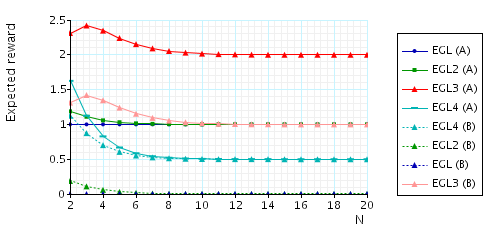
We have evaluated the fairness these protocols by calculating with PRISM the following fairness measures as the number of secrets n varies. Note that, under the assumption that all the secrets have the same number of bits, these results are independent of the number of bits L in each secret.
Note that all experiments were performed using PRISM's MTBDD engine.
The probability of reaching a state where A (B) does not know a pair while B (A) does knows a pair. This measure can be interpreted as the "chance" that the protocol is unfair towards either party. The corresponding PCTL property is given by:
In the graph below we have plotted these probability values as N (the number of pairs of secrets) varies.
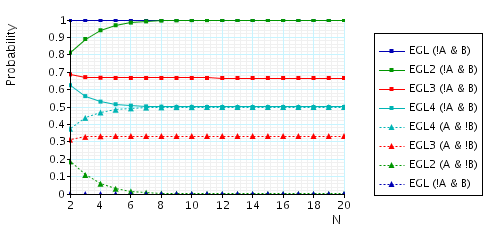
The expected number of bits that A needs in order to know a pair once B (A) knows a pair. This property is a quantification of how unfair the protocol is with respect to either party. To verify this property, in the case of the EGL protocol, for N=5 and party A (the other cases are similar), we make the following changes to the PRISM module "protocol":
module protocol b : [1..L]; // counter for current bit to be send n : [0..N-1]; // counter for which secret to send phase : [1..4]; // phase of the protocol // 1 - sending secrets using OT (step 1 of the protocol) // 2 - send bits of the secrets 0,...,N-1 (step 2 of the protocol) // 3 - send bits of the secrets N,...,2N-1 (step 2 of the protocol) party : [1..2]; // which party sends next (1 - A and 2 - B) // STEP 1 // A sends [receiveB] phase=1 & party=1 -> (party'=2); // B sends and we move onto the next secret [receiveA] phase=1 & party=2 & n<N-1 -> (party'=1) & (n'=n+1); // B sends and finished this step [receiveA] phase=1 & party=2 & n=N-1 -> (party'=1) & (phase'=2) & (n'=0); // STEP 2 (A sends) // next secret [receiveB] !kB & (phase=2 | phase=3) & party=1 & n<N-1-> (n'=n+1); // move onto secrets N,...,2N-1 [receiveB] !kB & phase=2 & party=1 & n=N-1 -> (phase'=3) & (n'=0); // move onto party B [receiveB] !kB & phase=3 & party=1 & n=N-1 -> (phase'=2) & (party'=2) & (n'=0); // STEP 2 (B sends) // next secret [receiveA] !kB & (phase=2 | phase=3) & party=2 & n<N-1 -> (n'=n+1); // move onto secrets N,...,2N-1 [receiveA] !kB & phase=2 & party=2 & n=N-1 -> (phase'=3) & (n'=0); // move onto next bit [receiveA] !kB & phase=3 & party=2 & n=N-1 & b<L -> (phase'=2) & (party'=1) & (n'=0) & (b'=b+1); // finished protocol [receiveA] !kB & phase=3 & party=2 & n=N-1 & b=L -> (phase'=4); // when B knows a pair we stop and compute the expected bits A requires [finish] kB & phase<4 -> (phase'=4); // FINISHED [] phase=4 -> (phase'=4); // loop endmodule
and add the following reward structure to the description:
// reward structure // cost is the number of bits A requires to know a pair formula cost = min(L-min(b0,b5),L-min(b1,b6),L-min(b2,b7),L-min(b3,b8),L-min(b4,b9)); rewards "bits_A_needs" [finish] true : cost; endrewards
and then verify the formula R{"bits_A_needs"}=?[ F phase=4].
In the graph below we have plotted these expected values as N (the number of pairs of secrets) varies.
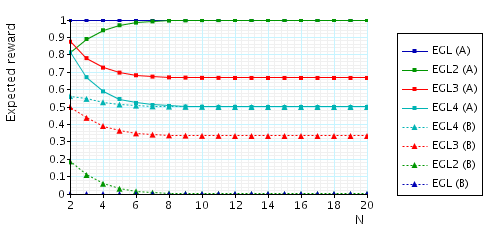
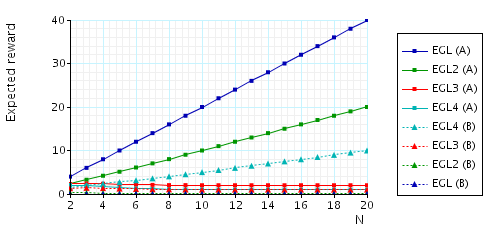
The expected number of messages from B (A) that A (B) needs in order to know a pair once B (A) knows a pair. This measure can be interpreted as an indication of how much influence a corrupted party has on the fairness of the protocol, since a corrupted party can try and delay these messages in order to gain an advantage. To verify this property, in the case of the EGL protocol and for party A (the other cases are similar), we add the following reward structure to the PRISM description:
// reward structure rewards "messages_A_needs" [receiveA] kB & !kA : 1; endrewards
and then verify the formula R{"messages_A_needs"}=?[F phase=4].
In the graph below we have plotted these expected values as N (the number of pairs of secrets) varies.
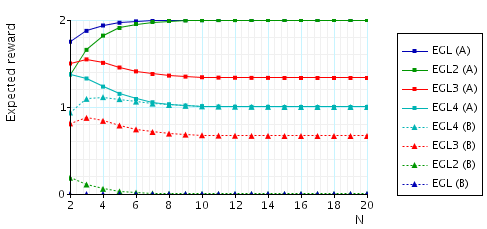
The expected number of messages that need to be sent (by either party) before A (B) knows a pair once B (A) knows a pair. This measure can be interpreted as representing the "duration" of unfairness, i.e, the time that one of the parties has an advantage. To verify this property, in the case of the EGL protocol and for party A (the other cases are similar), we add the following reward structure to the PRISM description:
// reward structure rewards "messages_until_A_knows" [receiveA] kB & !kA : 1; [receiveB] kB & !kA : 1; endrewards
and then verify the formula R{"messages_until_A_knows"}=?[F phase=4].
In the graph below we have plotted these expected values as N (the number of pairs of secrets) varies.
Summarizing the results presented in above, we observe that the protocol EGL4 appears to be the "fairest" protocol, except for the following: if the protocol ends up being unfair to B during a particular execution, this unfairness has the longest expected duration. Having said this, most of this is the time spent by B sending messages. Therefore, B can reduce this bias by sending his messages quickly.
An easy way to rectify this problem is to require that, whenever a party has to send a sequence of bits in a row (without the other party sending bits in between), these bits must be sent in a single message. For example, for EGL2 this would mean that A has to transmit the first bits of all the secrets 1,...,n to B in a single message at the start of step 2.
Below we present the effect this change would have on the performance of each of the variants we have considered. We only show the measures related to the expected number of messages as the other measures are not affected by this change. Note that this has no effect on the protocol EGL3 because it is fully interleaved: after a party has sent a single bit, the next transmission is from the other party. As the results indicate, this does indeed solve the fairness issues we found with the protocol EGL4. The limitation of this approach is that the size of messages increases as the number of secrets increases. Party B (A) is required to send a message containing n (n-1) bits.
The expected number of messages from B (A) that A (B) needs to knows a pair once B (A) knows a pair.
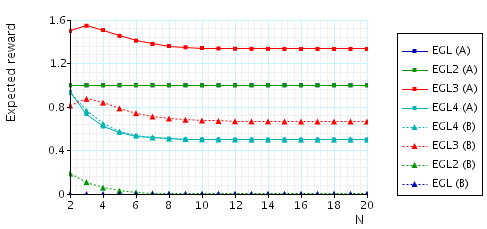
The expected number of messages that need to be sent (by either party) before A (B) knows a pair once B (A) knows a pair.