Related publications: [KNPS20]
Repeated public good games are a well studied model of social choice in economics. See, for example, the survey [Led95] and recent paper [HHCN19]. In the basic version of this game, a group of players each receives an endowment in each round and every player chooses how much of this to share with the group and how much to keep for themselves. The amounts that the players share with the group are combined and then multiplied by a factor f and then the resulting amount is shared equally between the players.
More formally, assuming there are two players and in a round each player i decides to contributes a share si of their endowment ei, then at the end of the round player i will receive in total:
i.e., the share of the player's endowment it keeps for itself plus the return it gets from the part it shares with the group.
We consider a concurrent stochastic game (CSG) model where each player receives a fixed endowment as its initial capital and then in any round the player can choose to share a portion of its current capital. To keep the model finite state, we allow each player to share only fixed fractions of their capital. In the model presented below, a player can either share all, three quarters, one half, one quarter or none of its current capital.
The model contains a module for each player which keeps track of both the players overall capital and the share it decides to invest in a round. The updates of the capital of each player, i.e., the variable c1 and c2, are dependent on the amount each player decided to invest in the current round and therefore thier updates use the primed values of the corresponding variable, i.e. the primed value of the variable s1 and s2.
There is an additional module that keeps track of the number of rounds that have been completed. Since this modules updates are independent of the choices of the players the commands of this module are unlabelled.
The model contains two reward structures for each player: the first returns for any state the current profit of that player (the current capital minus its initial capital); the second returns the final profit of the player once all rounds have been completed.
// public good game // players have an initial endowment // then in each round can share a portion of their current capital // the shares of the players are combined and the return is distributed equally // gxn/ghrs 22/01/20 csg player p1 m1 endplayer player p2 m2 endplayer const int n = 2; // number of players const int kmax; // number of rounds const int emax; // cap on the capital held by each player const int einit; // initial endowment const double f; // multiplier // round counter module counter k : [0..kmax+1] init 0; // round [] k<=kmax -> (k'=k+1); endmodule // module for player 1 module m1 c1 : [0..emax] init einit; // capital of the player s1 : [0..emax] init 0; // amount to be shared [i1_0] k<kmax -> (s1'=0) & (c1'=min(emax,c1-s1'+floor((f/n)*(s1'+s2')))); [i1_25] k<kmax -> (s1'=floor(0.25*c1)) & (c1'=min(emax,c1-s1'+floor((f/n)*(s1'+s2')))); [i1_50] k<kmax -> (s1'=floor(0.5*c1)) & (c1'=min(emax,c1-s1'+floor((f/n)*(s1'+s2')))); [i1_75] k<kmax -> (s1'=floor(0.75*c1)) & (c1'=min(emax,c1-s1'+floor((f/n)*(s1'+s2')))); [i1_100] k<kmax -> (s1'=c1) & (c1'=min(emax,c1-s1'+floor((f/n)*(s1'+s2')))); [done1] k>=kmax -> (c1'=0) & (s1'=0); endmodule // module for player 2 module m2 = m1[c1=c2, s1=s2, s2=s1, i1_0=i2_0, i1_25=i2_25, i1_50=i2_50, i1_75=i2_75, i1_100=i2_100, done1=done2] endmodule // current profit for player 1 rewards "r1i" true : c1 - einit; endrewards // current profit for player 2 rewards "r2i" true : c2 - einit; endrewards // final profit for player 1 rewards "done1" k=kmax : c1 - einit; endrewards // final profit for player 2 rewards "done2" k=kmax : c2 - einit; endrewards
We consider the following two non-zero properties where each player tries to maximise their expected profit either after all rounds have been completed or at the end of a specific round. We will fix the cap on capital held by each player at emax=100 and the initial endowment for each player at einit=4.
// players maximise their final profit <<p1:p2>>max=?(R{"done1"}[F k=kmax+1] + R{"done2"}[F k=kmax+1]) // players maximise their profit at a specific round const int K; <<p1:p2>>max=?(R{"r1i"}[I=K] + R{"r2i"}[I=K])
We now analyse the values and strategies for the first property, where both players try to maximise their capital as the number of rounds and the parameter f vary.
First, in the graphs below we the have plotted the optimal values for the players over kmax = 2, 4 and 6 rounds, first as the parameter f varies between 0 and 2 and then zoomed in on the area where the values of the players vary. In each case we see, for values of f close to 1 the optimal choice for each player is not to share any of its capital in any round, while for values close to 2 the optimal choice for each player is to share all of their capital in every round. For other values of f, as we will see, then the optimal choice of the players is to share different amounts in different rounds and in some cases this choice can be probabilistic.






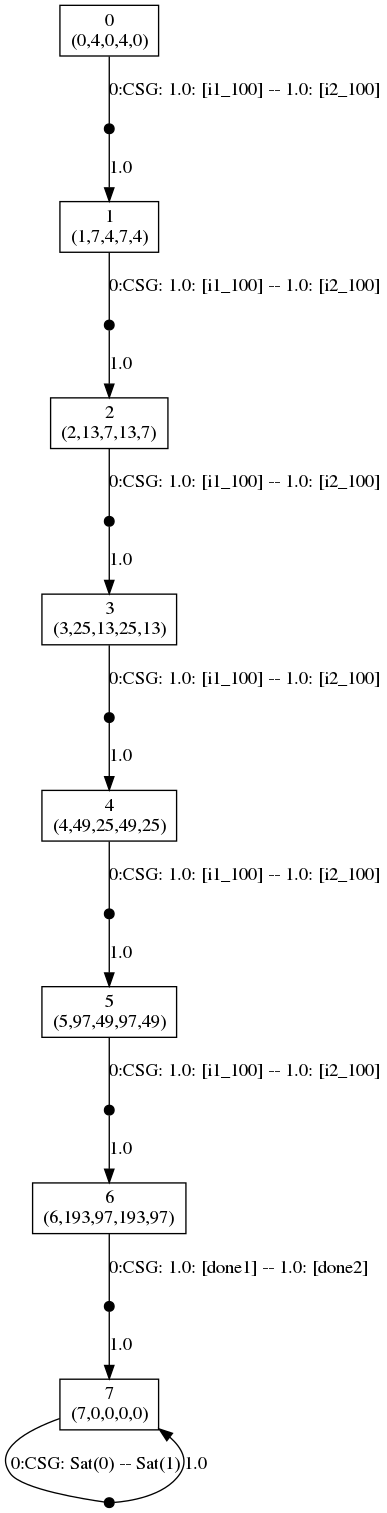
If f=1.78, then the following graph gives the optimal strategies for the two players (the dot files have been edited to replace floating point numbers with rationals to improve readability).
In the graph, the vertices correspond to the states of the game and are labelled with tuples corresponding to the values of the variables of the model: (k,c1,s1,c2,s2). The edges of the graph are labelled CSG followed by the choices for the two players (the probabilities of choosing available actions) with the choices for the different players separated by --. The graph is generated by running the command:
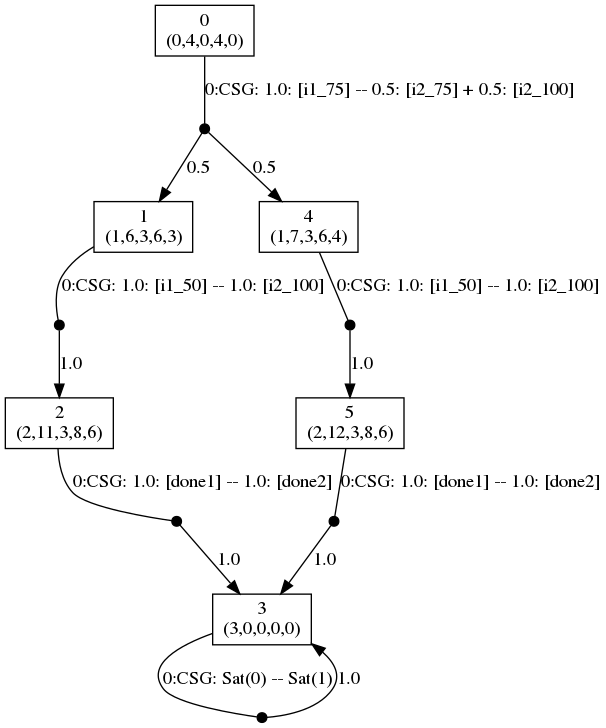
On the other hand, if f=1.80, then the optimal strategies are given below.
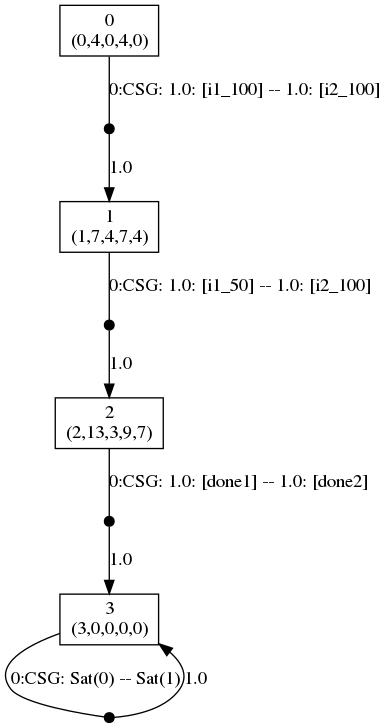
If f=1.91, then the following graph gives the optimal strategies for the two players.
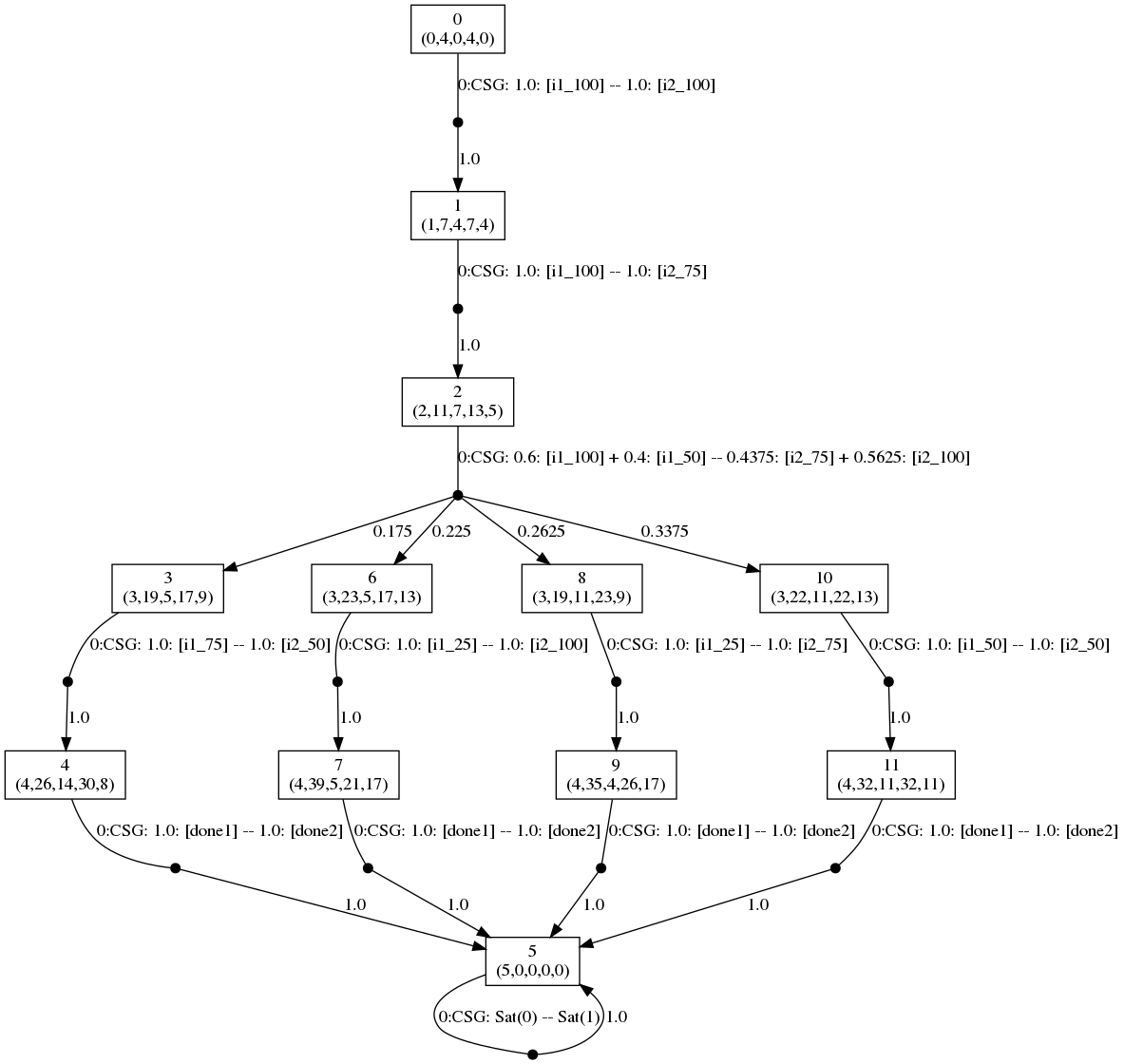
On the other hand, if f=1.92, then the optimal strategies are given below.
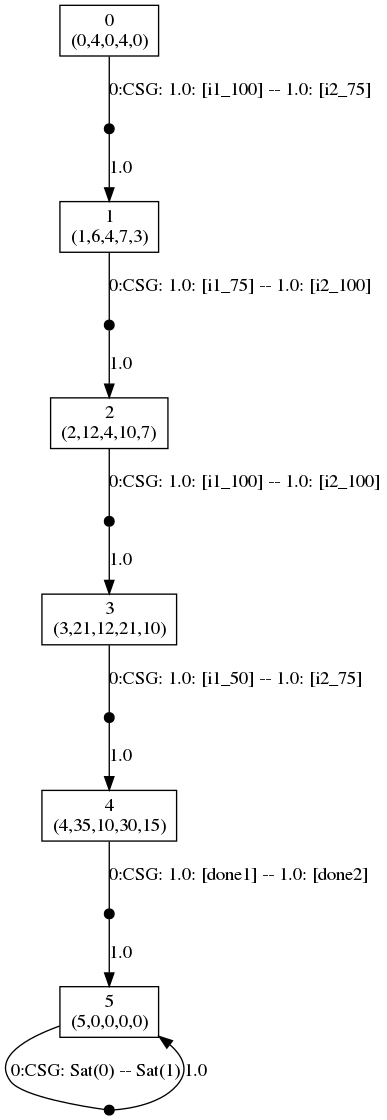
If f=1.98, then the following graph gives the optimal strategies for the two players.
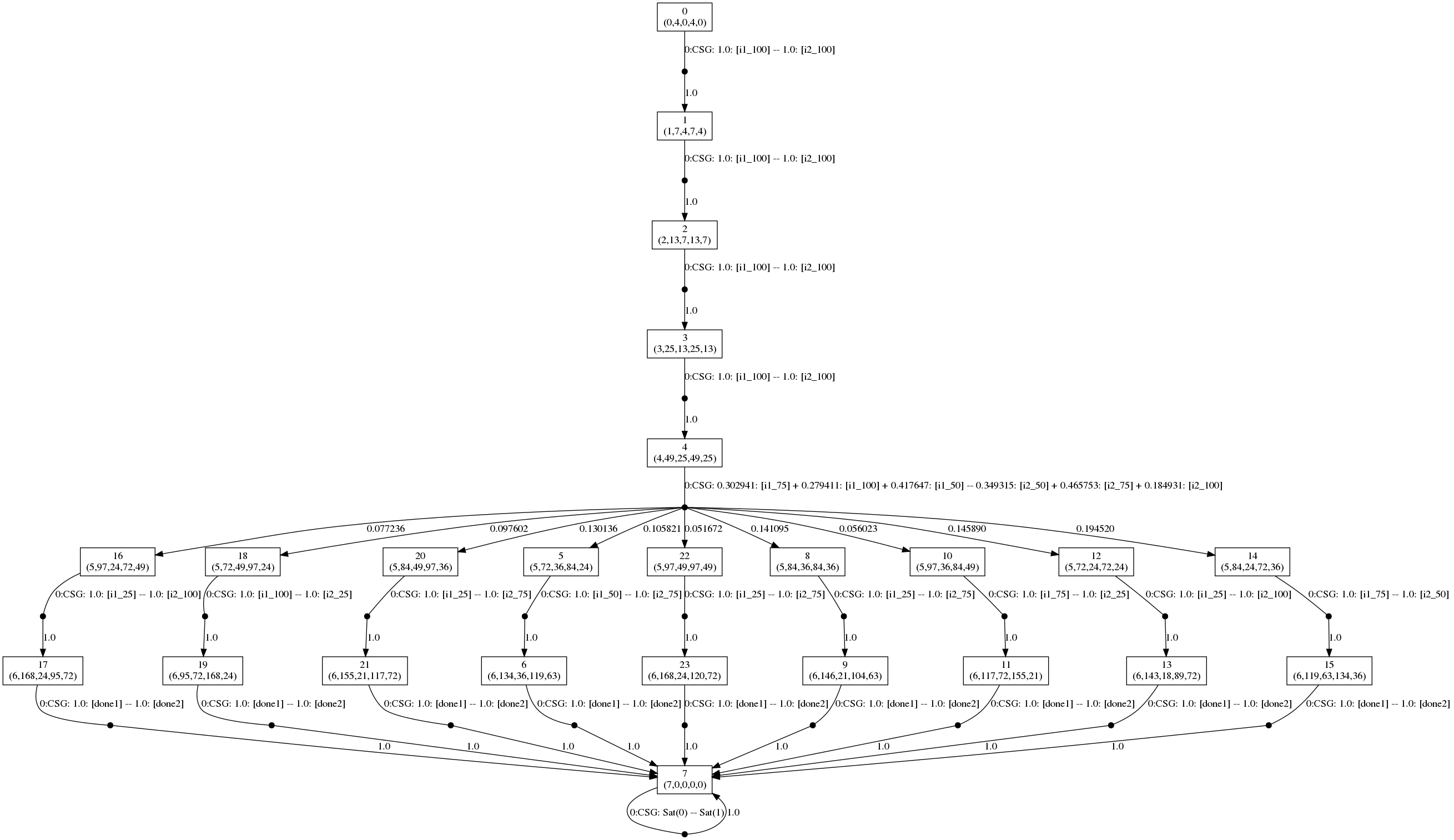
On the other hand, if f=1.99, then the optimal strategies are given below.