(Markowitch & Roggeman)
Related publications: [NPS13] [KNP19]
This case study analyses Markowitch & Roggeman’s non-repudiation protocol for information transfer [MR99]. Our models extend those presented previously in [LMST04]. One party, the originator O, sends information to a second party, the recipient R. Repudiation is defined as the denial of either party of having participated in all or part of the information transfer. For example, in electronic commerce, if the information represents the transfer of a service, then non-repudiation ensures the client (the recipient) cannot deny receiving the service as a reason for non-payment.
The protocol of Markowitch and Roggeman is probabilistic and does not require a trusted third party. It achieves the following non-repudiation properties:
The steps of the protocol are outlined below. First, to prevent replay attacks, the recipient R selects a date D which it sends, along with a request, to the originator O. Next, O randomly selects an integer n representing the number of steps of the protocol (which is never revealed to R during the execution) and computes functions fi such that their composition satisfies the following:
The composition operator ○ needs to be non-commutative to ensure that the recipient cannot start to compute the message until the final message f1(message) has been received.
To prevent the recipient from gaining an advantage, if the originator does not receive an acknowledgement within a certain time bound (denoted AD), the protocol is stopped and and the originator states that the recipient is trying to cheat. The time bound is chosen such that it is greater than the time it takes for a recipient to send a reply, but is not sufficient for the recipient to be able to compute the composition fn(message)○(···○ fi(message)···) for any i<n, i.e., the recipient does not have time to check if it has received the complete message before sending an acknowledgement.
|
The recipient chooses the date D 1. R → O: SignR(request,R,O,D) The originator checks D, chooses n and computes functions f1,...,fn 2. O → R: SignR(fn(message),O,R,D) 3. R → O: SignR(ack1) 4. O → R: SignR(fn-1(message),O,R,D) 5. R → O: SignR(ack2) ⋮ 2n. O → R: SignR(fn(message),O,R,D) 2n+1. R → O: SignR(ack1) |
We first model the protocol as a probabilistic timed automaton (PTA).
We assume that the choice of n is made by the recipient according to a geometric distribution with parameter p and the minimum time for the recipient to send an acknowledgement is ad.
We first consider when both parties act honestly and specify the protocol as the parallel composition of two PTAs, one representing the originator and one the recipient. These synchronise on the actions rec, send and ack, corresponding to the recipient initiating the transaction, the originator sending messages to the recipient and the recipient sending acknowledgements back.
The PRISM model of the honest version is presented below.
// non-repudiation protocol (with honest recipient) // Markowitch & Roggeman [MR99] // extended version of the PTA model from // R. Lanotte, A. Maggiolo-Schettini and A. Troina // Second Workshop Quantitative Aspects of Programming Languages (QAPL 2004), // ENTCS, vol. 112, pp. 113–129 (2005) pta // constants const double p; // parameter of geometric distribution (to generate number of messages) const int ad = 1; // min time to send an ack const int AD = 5; // deadline (if ack not arrived then end protocol) module originator o : [0..4]; // 0 - init // 1 - send // 2 - waiting // 3 - finished // 4 - error x : clock; // local clock invariant (o=0 => true) & (o=1 => x<=0) & (o=2 => x<=AD) & (o=3 => true) & (o=4 => true) endinvariant [req] o=0 -> (o'=1) & (x'=0); // init (receive a request from the recipient) [message] o=1 & x<=0 -> (o'=2); // send (send first message immediately) [ack] o=2 & x<AD -> 1-p : (o'=1) & (x'=0) // received an ack and not last + p : (o'=3) & (x'=0); // receive an ack and last [] o=2 & x>=AD -> (o'=4) & (x'=0); // ack not arrived within expected interval (stop) endmodule module recipient r : [0..2]; // 0 - request // 1 - wait // 2 - ack y : clock; // local clock invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => y<AD) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 & y>=ad -> (r'=1) & (y'=0); // send ack (which it always does) endmodule // received ack for final message sent label "terminated_successfully" = o=3;
The probabilistic choice in the originator correctly models selection of n according to a geometric distribution with parameter p, since the probability of each message being the last one to be sent is p. Notice that, in the PTA for the honest recipient, an acknowledgement is sent after between ad and AD time units.
We verify the following properties corresponding to successful termination.
// minimum probability terminate successfully Pmin=? [ F "terminated_successfully" ] const int T; // minimum probability that protocol terminates successfully by time T Pmin=? [ F<=T "terminated_successfully" ] // minimum probability that protocol terminates successfully by time T Pmax=? [ F<=T "terminated_successfully" ]
We find that the protocol does terminate with probability 1 and the following plots both the minimum and maximum probability of terminating by time T for p=0.01 and p=0.1. We see that increasing the parameter p improves the performance of the protocol when the parties behave honestly. However, as we shall see below, when the recipient behaves maliciously, increasing this parameter comes at a cost since it also increases the likelihood that the recipient gains an advantage.
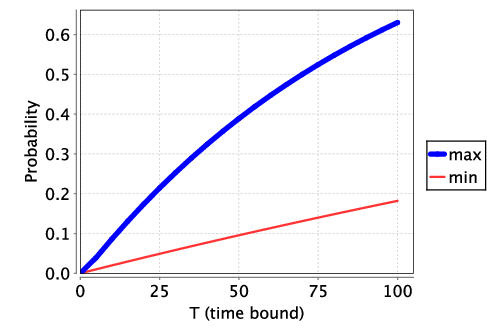
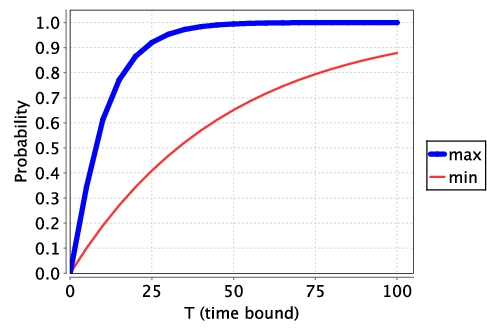
We next consider two versions of the protocol where the recipient can act maliciously In the first, the recipient can act maliciously (i.e., stop early by not returning an acknowledgement and trying to decode the message). We assume the time to decode the message is DECODE1. This corresponds to the PTA described in [LMST04], where the only malicious behaviour corresponds to stopping early.
The PRISM model is obtained by adding a constant, changing the recipient module and adding a label as shown below.
const int DECODE=8; // time to decode module malicious_recipient r : [0..5]; // 0 - request // 1 - wait // 2 - ack // 3 - try to decode // 4 - gains information (message was last) // 5 - does not gain information (message not last) y : clock; // local clock invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => true) & (r=3 => y<=10) & (r=4 => true) & (r=5 => true) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 -> (r'=1); // send ack (no time bound now as malicious) [] r=2 -> (r'=3) & (y'=0); // try and decode [] r=3 & y>=DECODE -> p : (r'=4) & (y'=0) // decode and last + (1-p) : (r'=5) & (y'=0); // decode and not last [ack] r=5 -> (r'=1) & (y'=0); // unsuccessful so try and continue endmodule // decodes last (nth) message label "gains_information" = r=4;
In the second, we introduce a more powerful malicious recipient, which has access to a method that takes time DECODE2 (which is less than AD) and with probability 0.25 correctly computes the composition while with probability 0.75 fails to compute the composition.
For this version the PRISM model is obtained by adding constants, changing the recipient module and adding a label as shown below.
const int DECODE1=8; // time to decode correctly const int DECODE2=4; // time to decode probabilistically module malicious_recipient r : [0..6]; // 0 - request // 1 - wait // 2 - ack // 3 - try to decode correctly // 4 - try to decode quickly (probabilistically) // 5 - decode correctly // 6 - failed to decode or decoded and not last y : clock; invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => true) & (r=3 => y<=DECODE1) & (r=4 => y<=DECODE2) & (r=5 => true) & (r=6 => true) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 -> (r'=1); // send ack (no time bound now as malicious) [] r=2 -> (r'=3) & (y'=0); // try and decode correctly [] r=2 -> (r'=4) & (y'=0); // try and decode fast [] r=3 & y>=DECODE1 -> p : (r'=5) & (y'=0) // decode and last + (1-p) : (r'=6) & (y'=0); // decode and not last [] r=4 & y>=DECODE2 -> p*0.25 : (r'=5) & (y'=0) // decode and last + (1-p)*0.25 : (r'=6) & (y'=0) // decode and not last + 0.75 : (r'=6) & (y'=0); // fail to decode // decoded and not last (continue by sending ack) // could combine with location 2, but would have the opportunity of decoding again // which is obviously a stupid thing to do so keep separate [ack] r=6 -> (r'=1) & (y'=0); endmodule // decodes last (nth) message label "gains_information" = r=5;
For these models we analyse the maximum probability that the recipient can gain knowledge both eventually and within a time bound as specified by the following properties.
const int T; // Maximum probability that malicious recepient gains information Pmax=? [ F "gains_information" ] // Maximum probability that malicious recepient gains information by deadline T Pmax=? [ F<=T "gains_information" ]
The following graph plots the maximum probability the recipient eventually gains knowledge as the parameter p varies. The plot demonstrates that the protocol is ε-fair with ε equal to p. Essentially, all this recipient can do to gain knowledge is to correctly guess which message is the last (which, when a message arrives, is true with probability p).
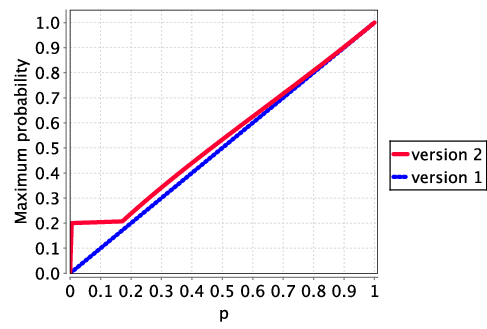
The following two graphs plot the maximum probability the recipient gains knowledge by a time bound as the parameter p varies for the two versions of the malicious recipient.
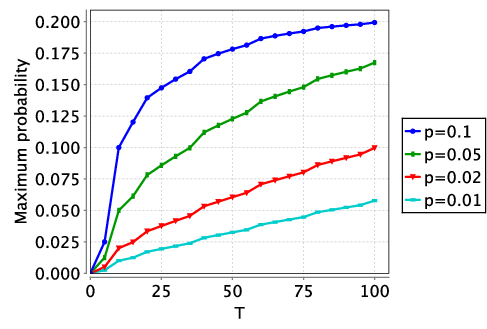
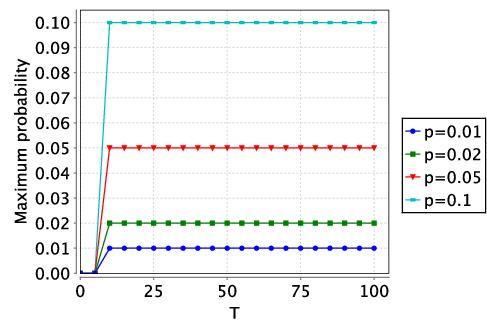
In the first graph, the probability of gaining an advantage over time remains constant after the arrival of the first message: since each message has an equal chance of being the last, there is nothing to be gained by waiting for a later one to try and decode. The figures also show that the malicious recipient in the second variant of the model (which has a chance of correctly decoding the message before the deadline) has a greater chance of gaining knowledge, thanks to its additional power.
We now extend the above and model the protocol as a two-player game. This allows both the originator and recipient to make choices which can depend on the history, i.e., the previous behaviour of the parties. The game is naturally turn-based since, in each round, first the originator sends a message after a delay of their choosing and, after receiving this message, the recipient can respond with an acknowledgement after a delay of their choosing. We therefore use turn-based probabilistic timed games (TPTGs) and PRISM-games.
TPTGs are an extension of PTAs to incorporate multiple players by allocating locations to different players. TPTGs are specified in PRISM-games in a similar fashion to (discrete-time) turn-based stochastic games (SMGs), by assigning modules and actions to players. The locations under the control of a specific player correspond to those for which the available actions or unlabelled transitions are under the control of that player.
We first extend the 'honest' version of the protocol where both O and R can choose delays for their messages but do follow the protocol (i.e., send messages and acknowledgements before timeouts occur). We assume the delay of messages is under the control of who send the message, and therefore assigning control of locations to either O or R, based on which party next sends a message. There is a complication in the location where O is waiting and R is sending an acknowledgement, as the delay before sending the acknowledgement controlled by R, while if the timeout is reached O should end the protocol. However, since O's behaviour is deterministic in this location, we assign this location to be under the control of R, but add the constraints that an acknowledgement can only be sent before the timeout is reached.
// non-repudiation protocol (with honest recipient) - turned-based game model // Markowitch & Roggeman [MR99] // extended version of the PTA model from // R. Lanotte, A. Maggiolo-Schettini and A. Troina // Second Workshop Quantitative Aspects of Programming Languages (QAPL 2004), // ENTCS, vol. 112, pp. 113–129 (2005) tptg // originator player o originator, [message] endplayer // recipient player r recipient, [req], [ack] endplayer // constants const double p; // parameter of geometric distribution (choose number of messages) const int ad = 1; // min time to send an ack const int AD = 5; // deadline (if ack not arrived then end protocol) const int md = 2; // min time to send a message const int MD = 9; // max time to send a message module originator o : [0..3]; // 0 - init // 1 - sending // 2 - waiting // 3 - finished x : clock; // local clock invariant (o=0 => true) & (o=1 => x<=MD) & (o=2 => x<=AD) & (o=3 => true) endinvariant [req] o=0 -> (o'=1) & (x'=0); // init (receive a request from the recipient) [message] o=1 & x>=md -> (o'=2) & (x'=0); // send (send first message immediately) [ack] o=2 & x<=AD -> 1-p : (o'=1) & (x'=0) // receive an ack and not last + p : (o'=3) & (x'=0); // receive an ack and last endmodule module recipient r : [0..2]; // 0 - requesting // 1 - waiting for message // 2 - sending ack y : clock; invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => y<=AD) // means has to send ack (honest) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 & y>=ad -> (r'=1) & (y'=0); // send ack (which it always does) endmodule // received ack for final message sent label "terminated_successfully" = o=3; rewards "time" true : 1; endrewards
The following properties specify the maximum probability the protocol terminates (both with and without a deadline) and the minimum expected time to termination different coalitions can ensure.
const int K; // Minimum probability that the protocol terminates successfully <<>>Pmax=? [ F "terminated_successfully" ] <<o>>Pmax=? [ F "terminated_successfully" ] <<r>>Pmax=? [ F "terminated_successfully" ] <<o,r>>Pmax=? [ F "terminated_successfully" ] // Maximum probability that the protocol terminates successfully within time K <<>>Pmax=? [ F<=K "terminated_successfully" ] <<o>>Pmax=? [ F<=K "terminated_successfully" ] <<r>>Pmax=? [ F<=K "terminated_successfully" ] <<o,r>>Pmax=? [ F<=K "terminated_successfully" ] // Minimum expected time for the protocol to terminate successfully <<>>Rmin=? [ F "terminated_successfully" ] <<o>>Rmin=? [ F "terminated_successfully" ] <<r>>Rmin=? [ F "terminated_successfully" ] <<o,r>>Rmin=? [ F "terminated_successfully" ]
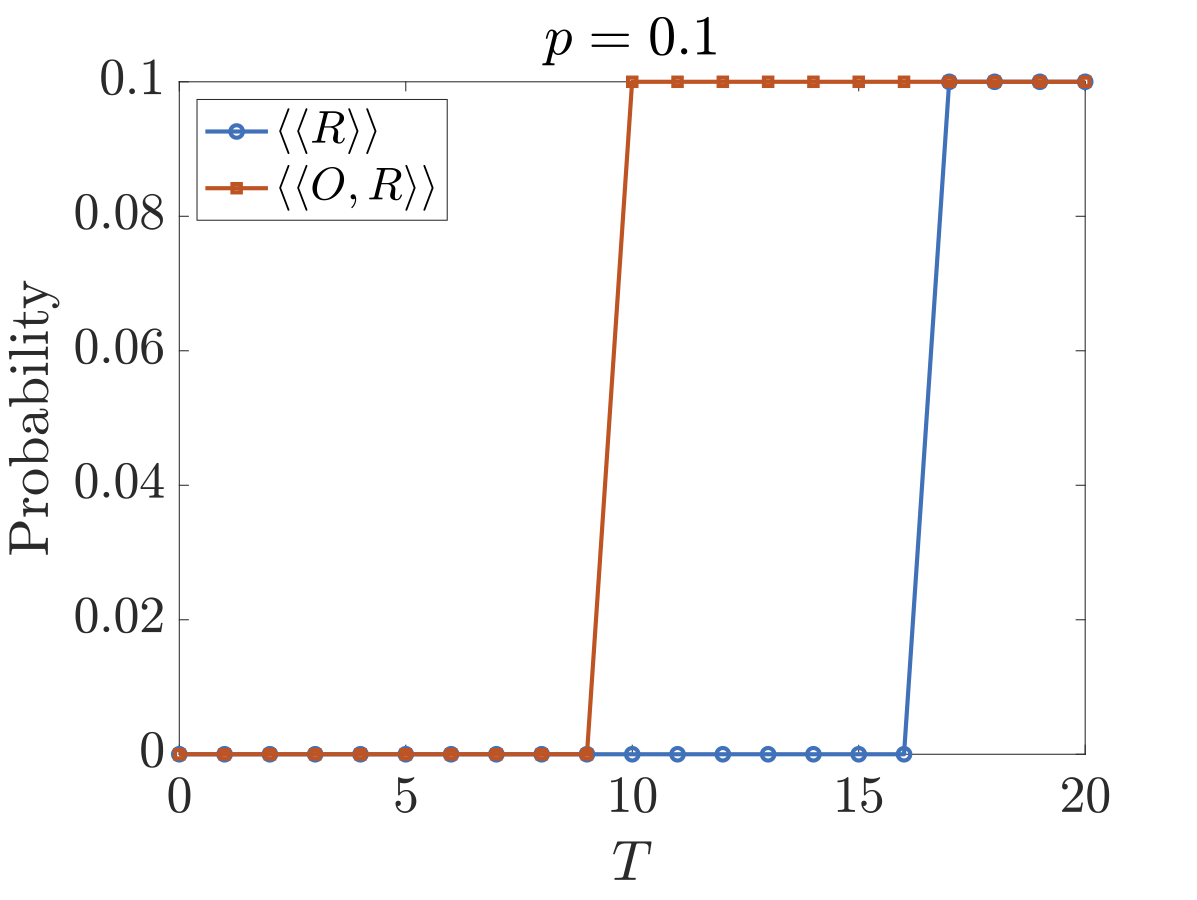
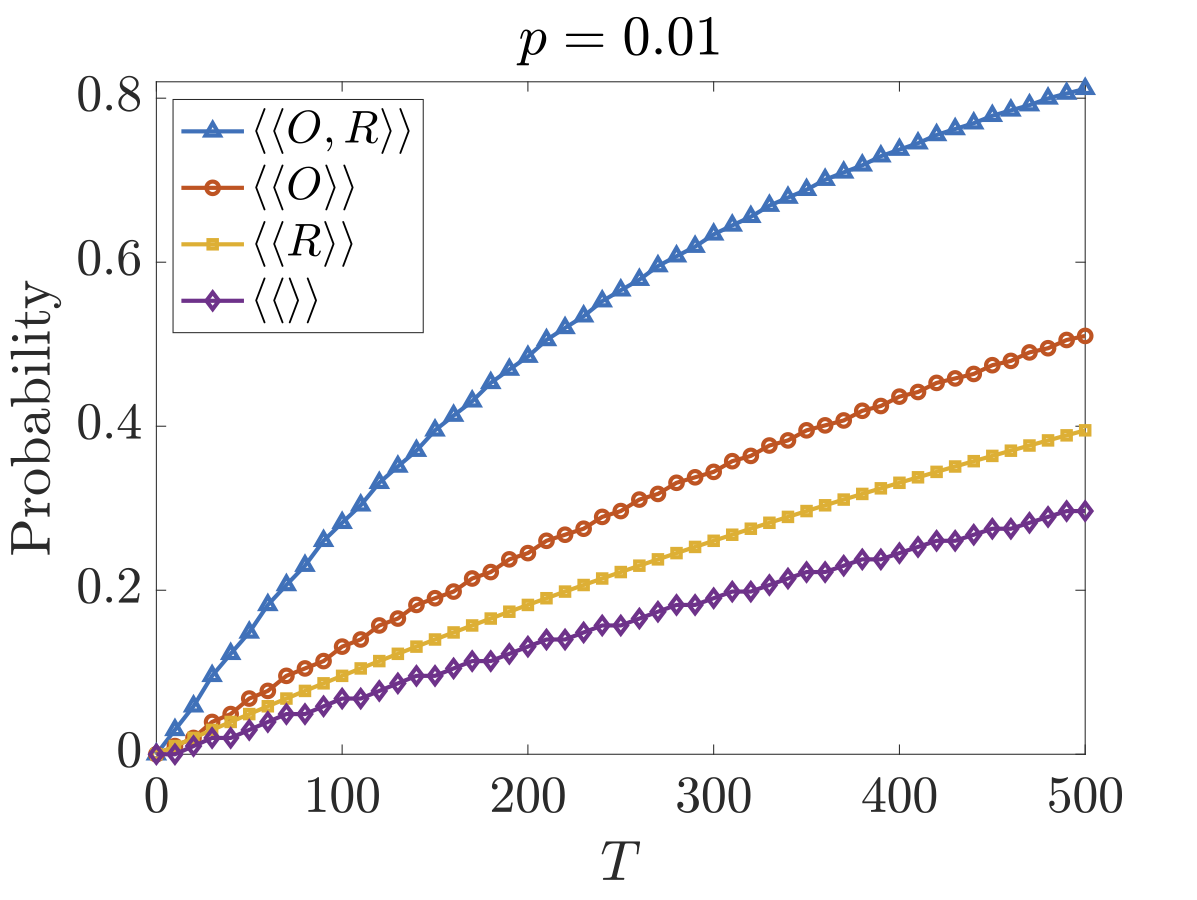
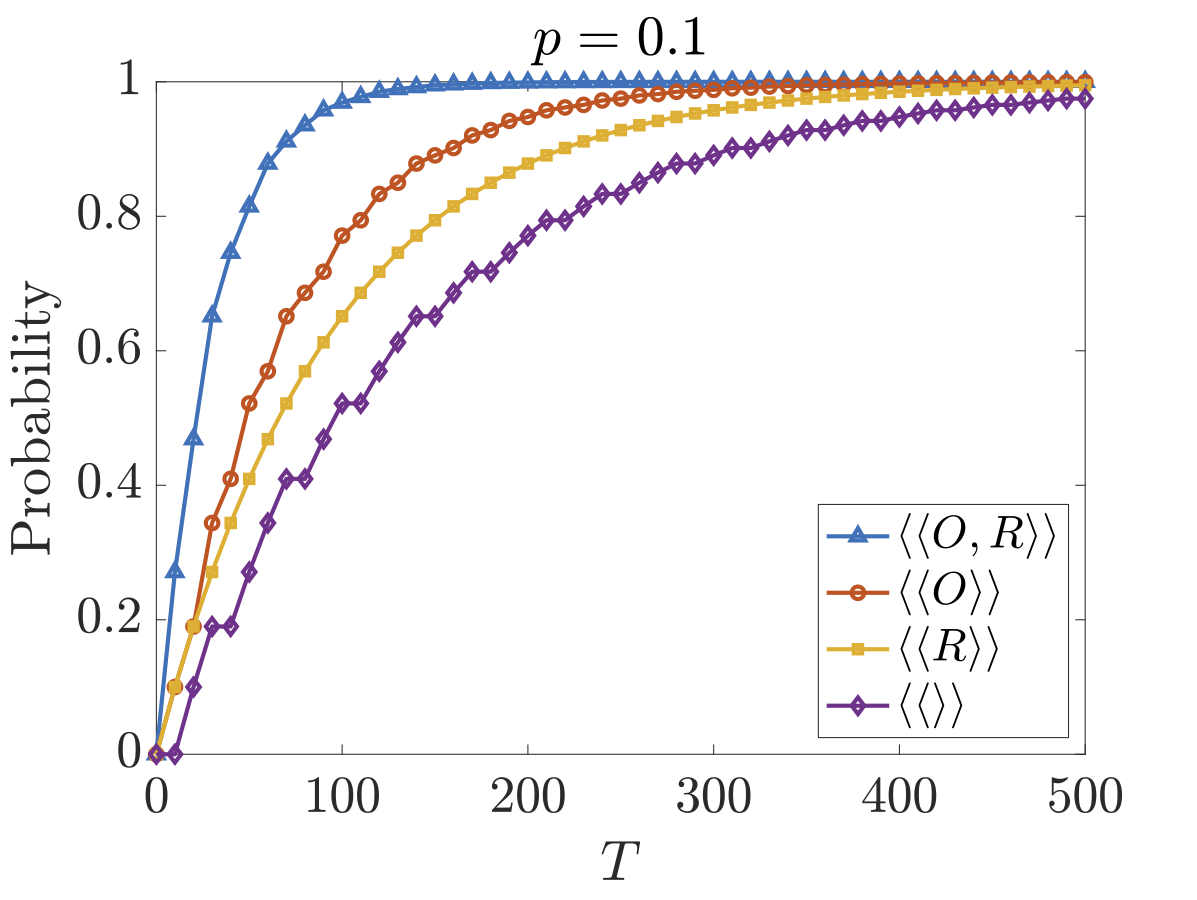
Below plots the results for these different coalitions for both the deadline property when p=0.01 and p=0.1 and expected time property for successful termination as the parameter p varies. As can be seen, both parties have some control over the time it takes for the protocol to complete and O has greater power as it can delay messages longer than R (if R delays too long then O will terminate the protocol stating R is cheating).


We also extend the two 'malicious' versions of the protocol. The TPTG models follow the same structure as that for the 'honest' version, requiring that, in the locations where O is waiting for an acknowledgement, once the timeout has been reached the only possible behaviour is for the protocol to terminate and O states R is trying to cheat.
// non-repudiation protocol (with malicious recipient) Markowitch & Roggeman [MR99] // extension and modification of the PTA model from R. Lanotte, A. Maggiolo-Schettini and A. Troina [LMT05] // malicious recipient can stop early tptg // originator player o originator, [message] endplayer // recipient player r recipient, [req], [ack], [end] endplayer // constants const double p; // parameter of geometric distribution (choose number of messages) const int ad = 1; // min time to send an ack const int AD = 5; // deadline (if ack not arrived then end protocol) const int md = 2; // min time to send a message const int MD = 9; // deadline (if message not arrived then end protocol) module originator o : [0..4]; // 0 - init // 1 - sending // 2 - waiting // 3 - finished // 4 - error x : clock; invariant (o=0 => true) & (o=1 => x<=MD) & (o=2 => x<=AD) & (o=3 => true) & (o=4 => true) endinvariant [req] o=0 -> (o'=1) & (x'=0); // receive a request from the recipient [message] o=1 & x>=md -> (o'=2) & (x'=0); // send message [ack] o=2 & x<=AD -> 1-p : (o'=1) & (x'=0) // receive an ack and not last + p : (o'=3) & (x'=0); // receive an ack and last [end] o=2 & x>=AD -> (o'=4) & (x'=0); // ack not arrived within expected interval (stop) endmodule module recipient r : [0..5]; // 0 - requesting // 1 - waiting for message // 2 - sending ack // 3 - decoding // 4 - sending ack after decoding // 5 - decoded and has complete message y : clock; invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => true) & (r=3 => y<=10) & (r=4 => true) & (r=5 => true) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 -> (r'=1); // send ack (no time bound now as malicious) [] r=2 -> (r'=3) & (y'=0); // decode // decoding (last and not last) [] r=3 & y>=8 -> p : (r'=5) & (y'=0) + (1-p) : (r'=4) & (y'=0); // decoded and not last (continue by sending ack) // could combine with location 2, but would have the opportunity of decoding again // which is obviously a stupid thing to do so keep separate [ack] r=4 -> (r'=1) & (y'=0); endmodule // decodes last (nth) message label "gains_information" = r=5; rewards "time" true : 1; endrewards
// non-repudiation protocol (with malicious recipient) Markowitch & Roggeman [MR99] // extension and modification of the PTA model from // R. Lanotte, A. Maggiolo-Schettini and A. Troina [LMT05] // malicious recipient can stop early and has a probabilistic decoder tptg // originator player o originator, [message] endplayer // recipient player r recipient, [req], [ack], [end] endplayer // constants const double p; // parameter of geometric distribution (choose number of messages) const int ad = 1; // min time to send an ack const int AD = 5; // deadline (if ack not arrived then end protocol) const int md = 2; // min time to send a message const int MD = 9; // deadline (if ack not arrived then end protocol) module originator o : [0..4]; // 0 - init // 1 - sending // 2 - waiting // 3 - finished // 4 - error x : clock; invariant (o=0 => true) & (o=1 => x<=MD) & (o=2 => x<=AD) & (o=3 => true) & (o=4 => true) endinvariant [req] o=0 -> (o'=1) & (x'=0); // receive a request from the recipient [message] o=1 & x>=md -> (o'=2) & (x'=0); // send message [ack] o=2 & x<=AD -> 1-p : (o'=1) & (x'=0) // receive an ack and not last + p : (o'=3) & (x'=0); // receive an ack and last [end] o=2 & x>=AD -> (o'=4) & (x'=0); // ack not arrived within expected interval (stop) endmodule module recipient r : [0..6]; // 0 - requesting // 1 - waiting for message // 2 - sending ack // 4 - decoding probabilistically but fast // 5 - decoding correctly // 6 - sending ack after decoding // 7 - decoded and has complete message y : clock; invariant (r=0 => y<=0) & (r=1 => true) & (r=2 => true) & (r=3 => y<=5) & (r=4 => y<=10) & (r=5 => true) & (r=6 => true) endinvariant [req] r=0 & y=0 -> (r'=1); // initiate protocol [message] r=1 -> (r'=2) & (y'=0); // receive message [ack] r=2 -> (r'=1); // send ack (no time bound now as malicious) [] r=2 -> (r'=3) & (y'=0); // decode probabilistically [] r=2 -> (r'=4) & (y'=0); // decode // decoding probabilistically (successfully and last, successfully and not last or unsuccessfully) [] r=3 & y>=4 -> p*0.25 : (r'=6) & (y'=0) + (1-p)*0.25 : (r'=5) & (y'=0) + 0.75 : (r'=2) & (y'=0); // decoding (last and not last) [] r=4 & y>=8 -> p : (r'=6) & (y'=0) + (1-p) : (r'=5) & (y'=0); // decoded and not last (continue by sending ack) // could combine with location 2, but would have the opportunity of decoding again // which is obviously a stupid thing to do so keep separate [ack] r=5 -> (r'=1) & (y'=0); endmodule // decodes last (nth) message label "gains_information" = r=6; rewards "time" true : 1; endrewards
The following properties express the the maximum probability the recipient gains information both with and without a deadline that different coalitions can ensure.
const int K; // Maximum probability that malicious recepient gains information <<r>>Pmax=? [ F "gains_information" ] <<o,r>>Pmax=? [ F "gains_information" ] // Maximum probability that malicious recepient gains information within time K <<r>>Pmax=? [ F<=K "gains_information" ] <<o,r>>Pmax=? [ F<=K "gains_information" ]
The figures below plot the maximum probability the recipient gains information by time T for versions 1 and 2 respectively. We have included the cases where O works against R (⟨⟨R⟩⟩) and where they collaborate (⟨⟨O,R⟩⟩). As we can see, although O cannot reduce the probability of R obtaining information, it can to some extent increase the time it takes R to obtain this information.