(Shapiro)
In this case study we consider a number of molecular reactions taken from Ehud Shapiro's lecture notes on Biomolecular Processes as Concurrent Computation.
In this approach, the time until a reaction between two molecules is modelled as an exponential distribution, and therefore we construct a CTMC model of the system where the states of the CTMC correspond to the number of molecules of each type and the transitions correspond to the possible reactions between the molecules. The rate of a reaction is determined by a base rate and the concentrations of the reactants (i.e. the number of each type of molecule that takes part in the reaction).
Note that, for each of the chemical reactions we consider, the rate of the reaction is the base rate multiplied by the product of the number of molecules of each type that take part in the reaction. Therefore, to model this is PRISM, we use the fact that in PRISM the rate of synchronous transition is defined as the product of the rates of the local transitions which form this synchronous transition.
The PRISM source code for this reaction is given below.
// Na + Cl <--> Na+ + Cl- // dxp/gxn 09/06/04 ctmc // constants const int N1; // number of Na molecules const int N2; // number of Cl molecules // Na and Na+ module module na na : [0..N1] init N1; // total number of Na and Na+ molecules is fixed at N1 // na is the number of Na molecules // therefore N1-na gives the number of Na+ molecules [e1] na>0 -> na : (na'=na-1); [e2] na<N1 -> (N1-na) : (na'=na+1); endmodule // Cl and Cl- module module cl cl : [0..N2] init N2; // total number of Cl and Cl- molecules is fixed at N2 // cl is the number of Cl molecules // therefore N2-cl is the number of Cl- molecules [e1] cl>0 -> cl : (cl'=cl-1); [e2] cl<N2 -> (N2-cl) : (cl'=cl+1); endmodule // base rates const double e1rate = 100; // Na + Cl -> Na+ + Cl- const double e2rate = 10; // Na+ + Cl- -> Na + Cl // module representing the base rates of reactions module base_rates [e1] true -> e1rate : true; [e2] true -> e2rate : true; endmodule // rewards: "percentage of Na molecules present (out of all Na/Na+ molecules)" rewards "percentage_na" true : 100*na/N1; endrewards
The table below shows statistics for the CTMCs we have built for different numbers values of the constants N1 and N2. The tables include:
| N1: | N2: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | |||||
| 10 | 10 | 11 | 20 | 247 | 21 | 0.061 | 11 | |||
| 20 | 20 | 21 | 40 | 577 | 41 | 0.065 | 21 | |||
| 40 | 40 | 41 | 80 | 1,317 | 81 | 0.104 | 41 | |||
| 60 | 60 | 61 | 120 | 1,967 | 81 | 0.159 | 61 | |||
| 80 | 80 | 81 | 160 | 2,957 | 161 | 0.280 | 81 | |||
| 100 | 100 | 101 | 200 | 3,695 | 201 | 0.351 | 101 | |||
| 250 | 250 | 251 | 500 | 10,231 | 501 | 2.742 | 251 | |||
Properties:
These properties are expressed in PRISM as follows.
// Constants: const double T; // time instant const int i; // number of molecules // Probability of there being i Na molecules at time T? P=? [ true U[T,T] na=i ] // Expected percentage of Na molecules at time T? R=? [ I=T ] // Expected long-run percentage of Na molecules? R=? [ S ]
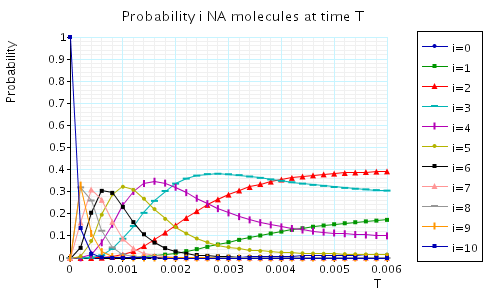
The following graph plots, in the case when N1=N2=10, the probability of there being i Na molecules at time as the value of T varies.
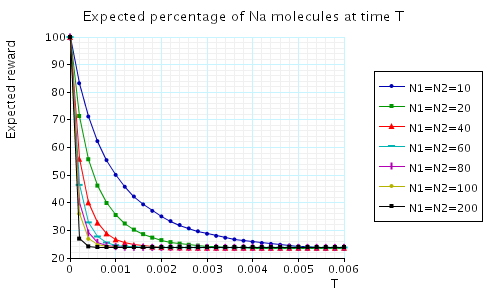
In the graph below we have plotted the expected values percentage of Na molecules at time T as T varies.
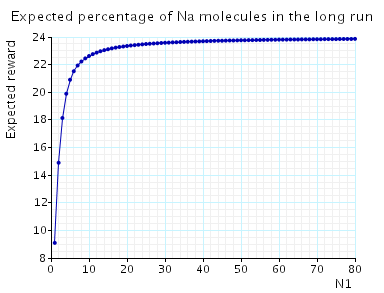
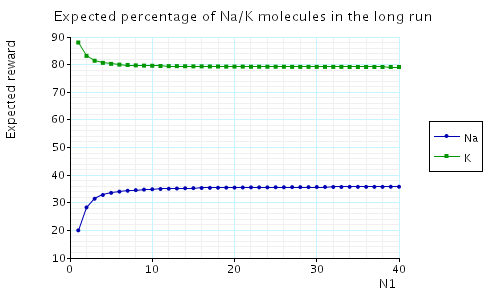
In the graph below we have plotted the expected long-run percentage of Na molecules as N1 varies.
The PRISM source code for this reaction is given below.
// K + Na + 2Cl <--> K+ + Na+ + 2Cl- // dxp/gxn 04/10/04 ctmc // constants const int N1; // number of Na molecules const int N2; // number of Cl molecules const int N3; // number of K molecules // Na and Na+ module module na na : [0..N1] init N1; // total number of Na and Na+ molecules is fixed at N1 // na is the number of Na molecules // therefore N1-na gives the number of Na+ molecules [e1] na>0 -> na : (na'=na-1); [e2] na<N1 -> (N1-na) : (na'=na+1); endmodule // Cl and Cl- module module cl cl : [0..N2] init N2; // total number of Cl and Cl- molecules is fixed at N2 // cl is the number of Cl molecules // therefore N2-cl is the number of Cl- molecules // reactions with Cl [e1] cl>0 -> cl : (cl'=cl-1); [e3] cl>0 -> cl : (cl'=cl-1); // reactions with CL- [e2] cl<N2 -> (N2-cl) : (cl'=cl+1); [e4] cl<N2 -> (N2-cl) : (cl'=cl+1); endmodule // K and K+ module module k k : [0..N3] init N3; // total number of K and K+ molecules is fixed at N3 // k is the number of K molecules // therefore N3-k gives the number of K+ molecules [e3] k>0 -> k : (k'=k-1); [e4] k<N3 -> (N3-k) : (k'=k+1); endmodule // base rates const double e1rate = 100; // Na + Cl -> Na+ + Cl- const double e2rate = 10; // Na+ + Cl- -> Na + Cl const double e3rate = 30; // K + Cl -> K+ + Cl- const double e4rate = 20; // K+ + Cl- -> K + Cl // module representing the base rates of reactions module base_rates dummy : bool; // dummy variable [e1] true -> e1rate : true; [e2] true -> e2rate : true; [e3] true -> e3rate : true; [e4] true -> e4rate : true; endmodule // reward structure (percentage of Na) rewards "percentage_na" true : 100*na/N1; endrewards // reward structure (percentage of K) rewards "percentage_k" true : 100*k/N3; endrewards
The table below shows statistics for the CTMCs we have built for different numbers values of the constants N1 and N2. The tables include:
| N1: | N2: | N3: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | ||||||
| 10 | 10 | 10 | 66 | 220 | 2,554 | 93 | 0.073 | 11 | |||
| 20 | 20 | 20 | 231 | 840 | 11,200 | 357 | 0.15 | 21 | |||
| 40 | 40 | 40 | 861 | 3,280 | 48,830 | 1,192 | 0.512 | 41 | |||
| 60 | 60 | 40 | 1,891 | 7,320 | 107,376 | 2,615 | 1.262 | 61 | |||
| 80 | 80 | 80 | 3,321 | 12,960 | 215,205 | 4,583 | 2.232 | 81 | |||
| 100 | 100 | 100 | 5,151 | 20,200 | 332,351 | 6,821 | 3.618 | 101 | |||
| 250 | 250 | 250 | 31,626 | 125,500 | 2,272,315 | 40,105 | 26.44 | 251 | |||
Properties:
These properties are expressed in PRISM as follows.
// Constants: const double T; // time instant const int i; // number of molecules // Probability of there being i Na/K molecules at time T? P=? [ true U[T,T] na=i ] P=? [ true U[T,T] k=i ] // Expected percentage of Na/K molecules at time T? R{"percentage_na"}=? [ I=T ] R{"percentage_k"}=? [ I=T ] // Expected long-run percentage of Na/K molecules? R{"percentage_na"}=? [ S ] R{"percentage_k"}=? [ S ]
The following graph plots, in the case when N1=N2=N3=10, the probability of there being i Na/K molecules at time T as the value of T varies.
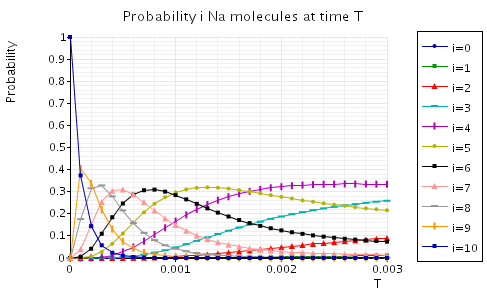
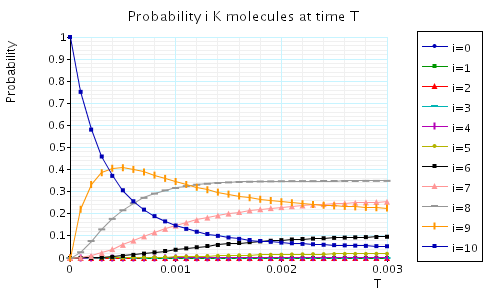
In the graph below we have plotted the expected percentage of Na/K molecules at time T as T varies.
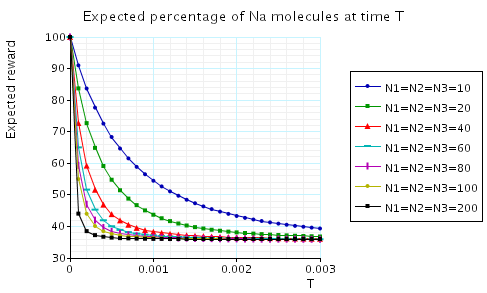
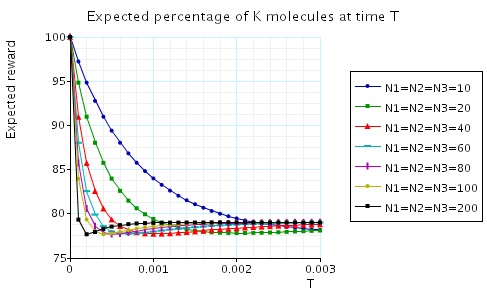
In the graph below we have plotted the expected long-run percentage of Na/K molecules as N1 varies.
The PRISM source code for this reaction is given below.
// Mg + 2Cl <--> Mg+2 + 2Cl- // dxp/gxn 04/10/04 ctmc // constants const int N1; // number of Mg molecules const int N2; // number of Cl molecules // Cl and Cl- module module cl cl : [0..N2] init N2; // total number of Cl and Cl- molecules is fixed at N2 // cl is the number of Cl molecules // therefore N2-cl is the number of Cl- molecules // reactions with Cl [e1] cl>0 -> cl : (cl'=cl-1); [e2] cl>0 -> cl : (cl'=cl-1); // reactions with CL- [e3] cl<N2 -> (N2-cl) : (cl'=cl+1); [e4] cl<N2 -> (N2-cl) : (cl'=cl+1); endmodule // Mg, Mg+ and Mg+2 module module mg mg : [0..N1] init N1; mg_p : [0..N1] init 0; // total number of Mg and Mg+ and Mg+2 molecules is fixed at N1 // mg is the number of Mg molecules // mg_p is the number of Mg molecules // therefore N1-(mg+mg+) gives the number of Mg+2 molecules [e1] mg>0 & mg_p<N1 -> mg : (mg'=mg-1) & (mg_p'=mg_p+1); [e2] mg_p>0 -> mg_p : (mg_p'=mg_p-1); [e3] mg_p>0 & mg<N1 -> mg_p : (mg'=mg+1) & (mg_p'=mg_p-1); [e4] mg_p+mg<N1 -> N1-(mg_p+mg) : (mg_p'=mg_p+1); endmodule // base rates const double e1rate = 10; // Mg + Cl --> Mg+ + Cl- const double e2rate = 100; // Mg+ + Cl --> Mg+2 + Cl- const double e3rate = 50; // Mg+ + Cl- --> Mg + Cl const double e4rate = 5; // Mg+2 + Cl- --> Mg+ + Cl- // module representing the base rates of reactions module base_rates dummy : bool; // dummy variable [e1] true -> e1rate : true; [e2] true -> e2rate : true; [e3] true -> e3rate : true; [e4] true -> e4rate : true; endmodule // reward structur: percentage of Mg molecules rewards "percentage_mg" true : 100*mg/N1; endrewards // reward structur: percentage of Mg+ molecules rewards "percentage_mgplus" true : 100*mg_p/N1; endrewards // reward structur: percentage of Mg+2 molecules rewards "percentage_mgplus2" true : max(100*(N1-(mg_p+mg))/N1,0); endrewards
The table below shows statistics for the CTMCs we have built for different numbers values of the constants N1 and N2. The tables include:
| N1: | N2: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | |||||
| 10 | 10 | 36 | 110 | 1,214 | 64 | 0.070 | 11 | |||
| 20 | 20 | 121 | 420 | 5,110 | 224 | 0.123 | 21 | |||
| 40 | 40 | 441 | 1,640 | 21,727 | 765 | 0.402 | 41 | |||
| 60 | 60 | 961 | 3,660 | 47,064 | 1,630 | 0.798 | 61 | |||
| 80 | 80 | 1,681 | 6,480 | 94,413 | 2,818 | 1.623 | 81 | |||
| 100 | 100 | 2,601 | 10,100 | 145,234 | 4,262 | 2.536 | 101 | |||
| 250 | 250 | 15,876 | 62,750 | 987,393 | 247,53 | 25.12 | 251 | |||
Properties:
These properties are expressed in PRISM as follows.
// Constants: const double T; // time instant const int i; // number of molecules // Probability of there being i Mg/Mg+/Mg+2 molecules at time T? P=? [ true U[T,T] mg=i ] P=? [ true U[T,T] mg_p=i ] P=? [ true U[T,T] N1-(mg_p+mg)=i ] // Expected percentage of Mg/Mg+/Mg+2 molecules at time T? R{"percentage_mg"}=? [ I=T ] R{"percentage_mgplus"}=? [ I=T ] R{"percentage_mgplus2"}=? [ I=T ] // Expected long-run percentage of Mg/Mg+/Mg+2 molecules? R{"percentage_mg"}=? [ S ] R{"percentage_mgplus"}=? [ S ] R{"percentage_mgplus2"}=? [ S ]
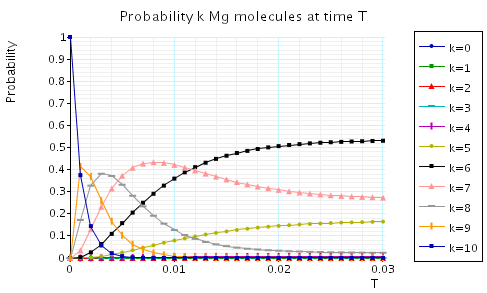
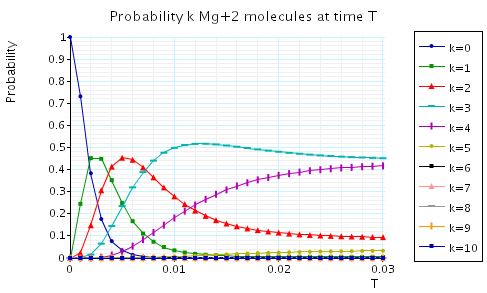
The following graph plots, in the case when N1=N2=10, the probability of there being i Mg and Mg+2 molecules at time T as the value of T varies.
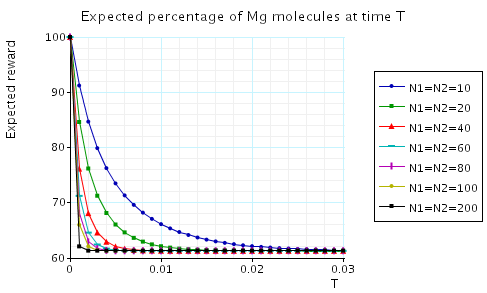
In the graphs below we have plotted the expected percentage of Mg and Mg+2 molecules at time T as T varies.
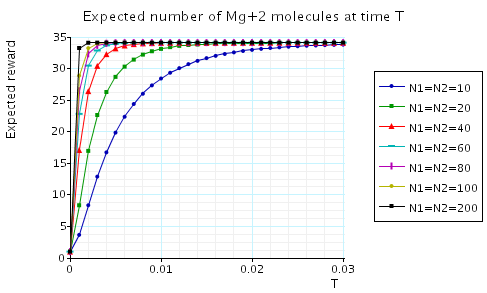
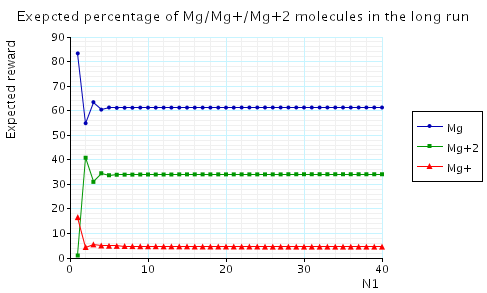
In the graph below we have plotted the expected long-run percentage of Mg/Mg+/Mg+2 molecules as N1 varies.