Related publications: [KNSW04, KNSW07]
This case study concerns probabilistic model checking of certain aspects of the IEEE 802.3 CSMA/CD (Carrier Sense, Multiple Access with Collision Detection) protocol. The CSMA/CD protocol is designed for networks with a single channel and specifies the behaviour of stations with the aim of minimising simultaneous use of the channel (data collision).
The basic structure of the protocol is as follows: when a station has data to send, it listens to the medium, after which, if the medium was free (no one transmitting), the station starts to send its data. On the other hand, if the medium was sensed busy, the station waits a random amount of time and then repeats this process.
This case study is used to test the feasibility of the symbolic (zone based) model checking algorithms introduced in [KNSW04, KNSW07] for checking probabilistic timed automata against PTCTL (Probabilistic Timed Computation Tree Logic) specifications. For comparison we also include the results obtained with the integer semantics approach in PRISM [KNS03b, KNPS03].
We now briefly summarise our prototype implementation of the model checking algorithms of [KNSW04, KNSW07]. It is important to note that the aim of our implementation is to validate the algorithms presented for model checking probabilistic timed automata against PTCTL, rather that to devise an efficient implementation; the latter will be the subject of future work.
The main step in the implementation of our techniques is the representation of (sets of) symbolic states and the operations required on them; more precisely, since a symbolic state is a pair (l,ζ) where l is a location of the probabilistic timed automaton and ζ is a zone (polyhedron), we require a method for representing zones and performing operations on zones.
Difference Bound Matrices (DBMs) [Dil89] are a well known data-structure for the representation of convex zones and are used in the model checkers UPPAAL and KRONOS. As the operations required by our algorithm can introduce non-convexity, we must represent non-convex zones. Following the approach presented in [Tri98], we represent non-convex zones by lists of DBMs, that is, we represent a non-convex zone ζ by a list of convex zones ζ1,...,ζn such that ζ= ζ1 ∪ ... ∪ ζn. It thus follows that a symbolic state can be represented by a location and a list of DBMs.
This representation is clearly not canonical: there are many ways of decomposing a non-convex zone into a set of convex zones. However, [Tri98] presents algorithms for the operations we require when zones are represented as lists of DBMs. Based on [Tri98], we have implemented, in Java, a prototype DBM package and the operations on lists of DBMs required by the model checking algorithms of [KNSW04, KNSW07].
The model we consider here is a probabilistic extension of the timed automata model given in [NSY92]. We consider the case when there are two stations trying to send data at the same time, and the overall model is given by the parallel composition of three probabilistic timed automata representing the medium and two stations trying to send data.
The probabilistic timed automaton representing the medium is given below.
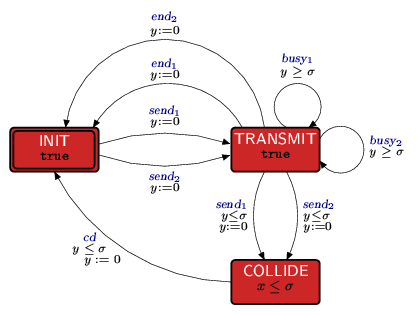
The medium is initially ready to accept data from any station (event send). Once a station starts sending its data there is an interval of time (at most σ), representing the time it takes for a signal to propagate between the stations, in which the medium will accept data from the other station (resulting in a collision). After this interval, if the other station tries to send data it will get the busy signal (busy). When a collision occurs, there is a delay (again at most σ) before the stations realize there has been a collision, after which the medium will become free (represented by the event cd). If the stations do not collide, then when a station finishes sending it data (event end) the medium becomes idle.
The probabilistic timed automaton representing a single station is given below. Note that, as in [NSY92] we assume that only packets of equal length are sent and we denote by λ the time to send a data packet.
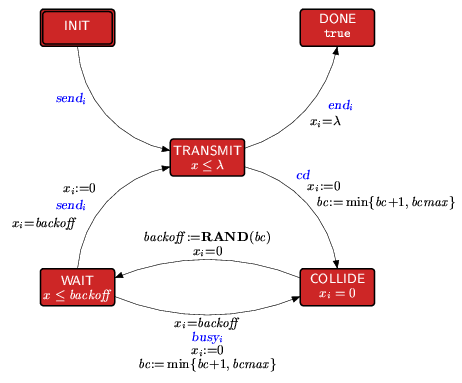
A station starts by sending is data (we are modelling the case when initially the stations collide). If there is no collision, then, after λ time units, the station finishes sending its data (event end). On the other hand, if there is a collision (event cd), the station attempts to retransmit the packet where the scheduling of the retransmission is determined by a truncated binary exponential backoff process. The delay before retransmitting is an integer number of time slots (each of length slotTime). The number of slots that the station waits after the nth transmission failure is chosen as a uniformly distributed random integer in the range:
where k=min(n,bcmax). Once this time has elapsed, if the medium appears free the station resends the data (event send), while if the medium is sensed busy (event busy) the station repeats this process.
Note that, to simplify the model, we have removed the limit on the number of times a station attempts to retransmit a packet as specified in the standard. For our experiments we consider the cases when bcmax is either 1 or 2.
The following parameters are taken from the IEEE standard 802.3 for 10 Mbps Ethernet.
We now report on the model checking results obtained using our prototype implementation for the following performance measures:
Since the algorithms work via backwards reachability and the model is constructed as the parallel composition of subcomponents, the prototype tool first performs a forwards reachability step to find the set of reachable locations (taking 19.77 seconds).
Due to the size of the deadline models, all experiments concerning the digital clocks approach were performed with PRISM's MTBDD engine.
The following probabilistic reachability property has been verified.
In PTCTL this is expressed by: P≥1[ true U done ]
The algorithm MaxV≥1 of [KNSW04, KNSW07]returns no symbolic states, which implies that the minimum probability is 1. Below we give the model checking statistics for MaxV≥1 as we vary the parameter c.
| c: | time (s): | MaxV≥1 iters: | MaxU≥1 iters: |
| 1 | 1,048 | 966 | 7,409 |
| 10 | 106.7 | 99 | 755 |
| 26 | 48.38 | 40 | 321 |
| 30 | 44.31 | 35 | 281 |
| 40 | 34.06 | 27 | 218 |
| 50 | 29.88 | 22 | 184 |
| 60 | 88.01 | 21 | 168 |
| 70 | 79.83 | 18 | 150 |
| 80 | 72.39 | 16 | 141 |
| 90 | 72.17 | 15 | 123 |
| 100 | 66.20 | 13 | 121 |
| 200 | 57.18 | 7 | 87 |
| 808 | 474.9 | 4 | 89 |
In contrast when using the digital clocks approach and PRISM, the model has 5,240 states, it takes 25.46 seconds to construct the model and 12.99 seconds to perform the verification.
| c: | |||
| time (s): | MaxV≥1 iters: | MaxU≥1 iters: | |
| 1 | 2,058 | 1,070 | 7,830 |
| 10 | 223.1 | 109 | 800 |
| 26 | 126.6 | 44 | 347 |
| 30 | 142.4 | 38 | 303 |
| 40 | 109.6 | 29 | 237 |
| 50 | 94.77 | 24 | 201 |
| 60 | 213.6 | 22 | 177 |
| 70 | 179.3 | 19 | 157 |
| 80 | 149.5 | 16 | 136 |
| 90 | 158.3 | 16 | 130 |
| 100 | 115.6 | 14 | 117 |
| 200 | 232.6 | 9 | 93 |
| 808 | 21,682 | 5 | 147 |
In contrast when using the digital clocks approach and PRISM, the model has 17,763 states, it takes 46.22 seconds to construct the model and 21.67 seconds to perform the verification.
We consider the following time-bounded probabilistic reachability property:
In PTCTL this is expressed by: z.P~λ[ true U done & z≤D ]
Maximum probabilities are computed through the algorithm MaxU (see [KNSW04, KNSW07]), where the final step requires the calculation of maximum reachability probabilities on a finite state system which we perform with PRISM.
| D: | MaxU | PRISM | maximum probability: | ||||
| time (s): | iters: | states: | construction time (s): | model checking | |||
| time (s): | iters: | ||||||
| 1000 | 1.177 | 9 | 71 | - | - | - | 0.0 |
| 1200 | 11.70 | 13 | 191 | - | - | - | 0.0 |
| 1400 | 26.51 | 17 | 311 | - | - | - | 0.0 |
| 1600 | 55.65 | 21 | 431 | - | - | - | 0.0 |
| 1800 | 76.68 | 32 | 617 | 7.633 | 0.075 | 47 | 0.729165 |
| 2000 | 84.33 | 38 | 725 | 9.112 | 0.123 | 58 | 0.929361 |
| 2200 | 98.82 | 48 | 861 | 13.54 | 0.192 | 71 | 0.988106 |
| 2400 | 120.5 | 58 | 997 | 17.98 | 0.259 | 84 | 0.997999 |
| 2600 | 145.3 | 68 | 1,129 | 26.50 | 0.362 | 92 | 0.999663 |
| 2800 | 174.2 | 78 | 1,263 | 35.59 | 0.446 | 99 | 0.999941 |
| 3000 | 239.8 | 88 | 1,399 | 42.36 | 0.534 | 99 | 0.999988 |
Below are the model checking statistics for the digital clocks approach when verifying this property with PRISM.
| D: | construction | model checking | maximum probability: | ||
| time (s): | states: | time (s): | iters: | ||
| 1000 | 141.7 | 1,876,105 | 0.074 | 0 | 0.0 |
| 1200 | 243.3 | 2,671,305 | 0.099 | 0 | 0.0 |
| 1400 | 307.8 | 3,546,505 | 0.12 | 0 | 0.0 |
| 1600 | 391.8 | 4,501,705 | 0.14 | 0 | 0.0 |
| 1800 | 445.5 | 5,528,692 | 291.1 | 1,846 | 0.729165 |
| 2000 | 513.8 | 6,570,692 | 612.5 | 2,013 | 0.929361 |
| 2200 | 583.5 | 7,612,692 | 847.1 | 2,234 | 0.988106 |
| 2400 | 658.2 | 8,654,692 | 969.1 | 2,455 | 0.997999 |
| 2600 | 670.2 | 9,696,692 | 1,229 | 2,673 | 0.999663 |
| 2800 | 700.2 | 10,738,692 | 1,486 | 2,886 | 0.999941 |
| 3000 | 764.3 | 11,780,692 | 1,703 | 3,097 | 0.999988 |
| D: | MaxU | PRISM | maximum probability: | ||||
| time (s): | iters: | states: | construction time (s): | model checking | |||
| time (s): | iters: | ||||||
| 1000 | 2.176 | 9 | 91 | - | - | - | 0.0 |
| 1200 | 178.0 | 11 | 423 | - | - | - | 0.0 |
| 1400 | 833.4 | 13 | 759 | - | - | - | 0.0 |
| 1600 | 192.6 | 15 | 1,095 | - | - | - | 0.0 |
| 1800 | 337.8 | 21 | 1,834 | 90.31 | 0.065 | 39 | 0.580428 |
| 2000 | 600.6 | 24 | 2,615 | 232.9 | 0.161 | 44 | 0.903011 |
| 2200 | 655.9 | 29 | 3,019 | 323.4 | 0.262 | 50 | 0.986651 |
| 2400 | 706.7 | 34 | 3,415 | 437.1 | 0.349 | 55 | 0.998157 |
| 2600 | 773.9 | 39 | 3,795 | 541.7 | 0.459 | 58 | 0.999743 |
| 2800 | 8,762 | 44 | 4,183 | 740.9 | 0.570 | 61 | 0.999961 |
| 3000 | 9,852 | 49 | 4,579 | 901.7 | 0.700 | 61 | 0.999990 |
Below are the model checking statistics for the digital clocks approach when verifying this property with PRISM.
| D: | construction | model checking | maximum probability: | ||
| time (s): | states: | time (s): | iters: | ||
| 1000 | 238.8 | 4,170,287 | 0.118 | 0 | 0.0 |
| 1200 | 331.5 | 5,813,169 | 0.152 | 0 | 0.0 |
| 1400 | 442.3 | 7,535,969 | 0.185 | 0 | 0.0 |
| 1600 | 532.8 | 9,338,769 | 0.219 | 0 | 0.0 |
| 1800 | 639.3 | 11,211,180 | 483.5 | 1,838 | 0.580428 |
| 2000 | 727.9 | 13,072,580 | 953.2 | 1,998 | 0.903011 |
| 2200 | 818.8 | 14,930,180 | 1,409 | 2,213 | 0.986651 |
| 2400 | 1,036 | 16,787,780 | 3,028 | 2,425 | 0.998157 |
| 2600 | 1,379 | 18,645,380 | 3,313 | 2,635 | 0.999743 |
| 2800 | 1,973 | 20,502,980 | 2,931 | 2,843 | 0.999961 |
| 3000 | 1,261 | 22,360,580 | 4,304 | 2,999 | 0.999990 |
Minimum probabilities are computed through the algorithms MaxV≥1 and MaxU, where the final step of the MaxU requires the calculation of maximum reachability probabilities which we again perform with PRISM.
For comparison we also consider an alternative approach for calculating minimum probabilities if deadline properties which reduces the problem to computing maximum probabilities on a modified model. More precisely, since eventually both stations send their packet correctly with probability 1, we can use the technique given in [KNS03b] and instead compute the minimum probability of satisfying the property
z.P~λ[ true U done & z≤D ]
as 1 minus the maximum probability of satisfying the formula
P~λ[ true U exceeded ]
on the probabilistic timed automaton after the following modifications have been performed.
| - | States in which done is true are forced to make a transition to a sink-location. |
| - | Add a transition to a different, ``deadline exceeded'' sink-location, denoted exceeded, as soon as the value of the clock z exceeds D in all states which do not satisfy done). |
We first consider the affect that the parameter c has on the performance of the MaxV≥1 algorithm when D=2000 and D=3000.
| c: | D=2000 | D=3000 | ||||
| time (s): | MaxV≥1 iters: | MaxU≥1 iters: | time (s): | MaxV≥1 iters: | MaxU≥1 iters: | |
| 1 | 269.6 | 132 | 1,062 | 274.5 | 132 | 1,062 |
| 10 | 31.94 | 15 | 126 | 33.14 | 15 | 126 |
| 26 | 21.60 | 9 | 94 | 23.85 | 9 | 94 |
| 30 | 27.75 | 9 | 94 | 28.87 | 9 | 94 |
| 40 | 18.20 | 7 | 78 | 22.14 | 7 | 78 |
| 50 | 18.67 | 6 | 70 | 19.56 | 6 | 70 |
| 60 | 201.2 | 8 | 91 | 191.8 | 8 | 91 |
| 70 | 199.3 | 8 | 91 | 217.3 | 8 | 91 |
| 80 | 182.4 | 7 | 84 | 186.1 | 7 | 84 |
| 90 | 179.5 | 7 | 84 | 198.6 | 7 | 84 |
| 100 | 189.3 | 7 | 84 | 186.5 | 7 | 84 |
| 200 | 83.67 | 6 | 90 | 96.07 | 6 | 90 |
| 808 | 659.5 | 5 | 115 | 587.8 | 5 | 115 |
We now give the overall model checking time of our implementation in the case the parameter c of the algorithm MaxV≥1 is set equal to 50.
| D: | MaxV≥1 | MaxU | PRISM | minimum probability: | |||||
| time (s): | iters: | time (s): | iters: | states: | construction time (s): | model checking | |||
| time (s): | iters: | ||||||||
| 1000 | 15.61 | 70 | 25.35 | 23 | 351 | 2.072 | 0.021 | - | 0.0 |
| 1200 | 15.71 | 70 | 25.58 | 23 | 351 | 1.842 | 0.021 | - | 0.0 |
| 1400 | 16.04 | 70 | 25.94 | 23 | 351 | 1.834 | 0.02 | - | 0.0 |
| 1600 | 15.92 | 70 | 25.72 | 23 | 351 | 1.836 | 0.021 | - | 0.0 |
| 1800 | 15.69 | 70 | 29.96 | 27 | 441 | 2.992 | 0.057 | 42 | 0.583332 |
| 2000 | 18.67 | 70 | 38.85 | 37 | 591 | 6.454 | 0.073 | 52 | 0.869791 |
| 2200 | 15.64 | 70 | 54.03 | 46 | 783 | 11.63 | 0.098 | 65 | 0.966390 |
| 2400 | 15.59 | 70 | 82.11 | 53 | 975 | 18.69 | 0.134 | 75 | 0.991279 |
| 2600 | 15.58 | 70 | 118.1 | 61 | 1,143 | 29.08 | 0.153 | 86 | 0.997256 |
| 2800 | 15.63 | 70 | 172.5 | 68 | 1,335 | 40.12 | 0.206 | 98 | 0.999298 |
| 3000 | 19.56 | 70 | 258.7 | 77 | 1,527 | 53.69 | 0.228 | 108 | 0.999819 |
Next we give model checking statistics for the approach for computing the maximum probability of satisfying P~λ[ true U exceeded ] on the modified automaton.
| D: | MaxU | PRISM | maximum probability: | ||||
| time (s): | iters: | states: | construction time (s): | model checking | |||
| time (s): | iters: | ||||||
| 1000 | 11.44 | 29 | 362 | 2.843 | 0.065 | - | 1 |
| 1200 | 11.49 | 29 | 362 | 2.704 | 0.039 | - | 1 |
| 1400 | 11.48 | 29 | 362 | 2.682 | 0.044 | - | 1 |
| 1600 | 11.46 | 29 | 362 | 2.675 | 0.038 | - | 1 |
| 1800 | 14.76 | 33 | 440 | 4.147 | 0.097 | 42 | 0.416668 |
| 2000 | 20.08 | 43 | 562 | 8.234 | 0.127 | 52 | 0.130209 |
| 2200 | 37.24 | 52 | 722 | 13.28 | 0.184 | 65 | 0.033610 |
| 2400 | 75.31 | 59 | 882 | 20.04 | 0.177 | 75 | 0.008720 |
| 2600 | 103.0 | 67 | 1,022 | 27.09 | 0.205 | 86 | 0.002744 |
| 2800 | 182.7 | 74 | 1,182 | 41.27 | 0.241 | 98 | 7.012e-4 |
| 3000 | 261.2 | 83 | 1,342 | 53.06 | 0.281 | 108 | 1.799e-4 |
Below are the model checking statistics for the digital clocks approach.
| D: | construction | model checking | minimum probability: | ||
| time (s): | states: | time (s): | iters: | ||
| 1000 | 141.7 | 1,876,105 | 0.269 | 0 | 0.0 |
| 1200 | 243.3 | 2,671,305 | 0.321 | 0 | 0.0 |
| 1400 | 307.8 | 3,546,505 | 0.441 | 0 | 0.0 |
| 1600 | 391.8 | 4,501,705 | 0.473 | 0 | 0.0 |
| 1800 | 445.5 | 5,528,692 | 333.3 | 1,841 | 0.583332 |
| 2000 | 513.8 | 6,570,692 | 746.2 | 2,030 | 0.869791 |
| 2200 | 583.5 | 7,612,692 | 1,052 | 2,252 | 0.966390 |
| 2400 | 658.2 | 8,654,692 | 1,159 | 2,468 | 0.991279 |
| 2600 | 670.2 | 9,696,692 | 1,472 | 2,657 | 0.997256 |
| 2800 | 700.2 | 10,738,692 | 1,737 | 2,873 | 0.999298 |
| 3000 | 764.3 | 11,780,692 | 2,020 | 3,089 | 0.999819 |
We first consider the affect that the parameter c has on the performance of the MaxV≥1 algorithm when D=2000 and D=3000.
| c: | D=2000 | D=3000 | ||||
| time (s): | MaxV≥1 iters: | MaxU≥1 iters: | time (s): | MaxV≥1 iters: | MaxU≥1 iters: | |
| 1 | 660.9 | 236 | 1,899 | 666.3 | 236 | 1,899 |
| 10 | 78.58 | 26 | 219 | 78.26 | 26 | 219 |
| 26 | 93.48 | 13 | 136 | 84.79 | 13 | 136 |
| 30 | 86.36 | 12 | 128 | 75.36 | 12 | 128 |
| 40 | 73.51 | 10 | 108 | 76.26 | 10 | 108 |
| 50 | 81.82 | 8 | 92 | 58.61 | 8 | 92 |
| 60 | 270.7 | 8 | 91 | 229.5 | 8 | 91 |
| 70 | 270.9 | 8 | 91 | 237.5 | 8 | 91 |
| 80 | 272.4 | 8 | 88 | 257.6 | 8 | 88 |
| 90 | 271.2 | 8 | 88 | 282.5 | 8 | 88 |
| 100 | 256.7 | 8 | 88 | 225.3 | 8 | 88 |
| 200 | 1,101 | 7 | 94 | 1,083 | 7 | 94 |
| 808 | 103,134 | 6 | 217 | 107,167 | 6 | 217 |
We now give the overall model checking time of our implementation in the case the parameter c of the algorithm MaxV≥1 is set equal to 50.
| D: | MaxV≥1 | MaxU | PRISM | minimum probability: | ||||||
| time (s): | iters: | time (s): | iters: | states: | construction time (s): | model checking | ||||
| time (s): | iters: | |||||||||
| 1000 | 58.06 | 92 | 174.5 | 16 | 724 | 13.77 | 0.024 | - | 0.0 | |
| 1200 | 63.03 | 92 | 179.3 | 16 | 724 | 13.38 | 0.024 | - | 0.0 | |
| 1400 | 72.61 | 92 | 187.9 | 16 | 724 | 13.35 | 0.024 | - | 0.0 | |
| 1600 | 63.26 | 92 | 181.2 | 16 | 724 | 13.36 | 0.023 | - | 0.0 | |
| 1800 | 59.27 | 92 | 1,371 | 19 | 1,203 | 46.47 | 0.066 | 36 | 0.387618 | |
| 2000 | 81.83 | 92 | 5,564 | 24 | 1,760 | 99.30 | 0.091 | 42 | 0.837514 | |
| 2200 | 60.50 | 92 | 6,394 | 29 | 2,170 | 164.7 | 0.129 | 51 | 0.972994 | |
| 2400 | 58.91 | 92 | 9,267 | 34 | 2,578 | 227.4 | 0.172 | 59 | 0.994852 | |
| 2600 | 77.00 | 92 | 1,2258 | 36 | 2,935 | 289.9 | 0.213 | 65 | 0.998839 | |
| 2800 | 65.12 | 92 | 1,5088 | 40 | 3,343 | 363.1 | 0.258 | 73 | 0.999791 | |
| 3000 | 58.20 | 92 | 1,6878 | 44 | 3,751 | 557.5 | 0.299 | 80 | 0.999960 | |
Next we give model checking statistics for the approach for computing the maximum probability of satisfying P~λ[ true U exceeded ] on the modified automaton.
| D: | MaxU | PRISM | maximum probability: | ||||
| time (s): | iters: | states: | construction time (s): | model checking | |||
| time (s): | iters: | ||||||
| 1000 | 171.8 | 21 | 737 | 18.232 | 0.040 | - | 1.0 |
| 1200 | 169.0 | 21 | 737 | 18.316 | 0.041 | - | 1.0 |
| 1400 | 163.0 | 21 | 737 | 18.572 | 0.041 | - | 1.0 |
| 1600 | 164.0 | 21 | 737 | 18.51 | 0.041 | - | 1.0 |
| 1800 | 589.9 | 25 | 1,208 | 63.309 | 0.126 | 36 | 0.612381 |
| 2000 | 1,374 | 30 | 1,751 | 135.44 | 0.176 | 42 | 0.162485 |
| 2200 | 2,104 | 35 | 2,145 | 219.56 | 0.222 | 51 | 0.027004 |
| 2400 | 3,301 | 40 | 2,537 | 296.64 | 0.269 | 59 | 0.005147 |
| 2600 | 5,144 | 41 | 2,880 | 383.48 | 0.311 | 65 | 0.001159 |
| 2800 | 7,875 | 46 | 3,272 | 486.72 | 0.369 | 73 | 2.071e-4 |
| 3000 | 9,835 | 50 | 3,664 | 603.34 | 0.445 | 80 | 0.380e-4 |
Below are the model checking statistics for the digital clocks approach.
| D: | construction | model checking | minimum probability: | ||
| time (s): | states: | time (s): | iters: | ||
| 1000 | 238 | 4,170,287 | 0.431 | 0 | 0.0 |
| 1200 | 331 | 5,813,169 | 0.519 | 0 | 0.0 |
| 1400 | 442 | 7,535,969 | 0.466 | 0 | 0.0 |
| 1600 | 532 | 9,338,769 | 0.578 | 0 | 0.0 |
| 1800 | 639 | 11,211,180 | 512.1 | 1,835 | 0.387618 |
| 2000 | 727 | 13,072,580 | 1,180 | 2,020 | 0.837514 |
| 2200 | 818 | 14,930,180 | 1,777 | 2,234 | 0.972994 |
| 2400 | 1,036 | 16,787,780 | 2,170 | 2,448 | 0.994852 |
| 2600 | 1,379 | 18,645,380 | 2,818 | 2,633 | 0.998839 |
| 2800 | 1,973 | 20,502,980 | 5,476 | 2,843 | 0.999791 |
| 3000 | 1,261 | 22,360,580 | 4,941 | 3,051 | 0.999960 |